Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.6 - Ex. 43b
Para encontre:
O usando uma tabela de valores.
Passo 1
Bom galera, o limite que a questão quer que a gente calcule é:
Passo 2
Beleza, então vamor fazer uma tabela de valores altos e crescentes aplicados nessa função, podemos fazer isso na calculadora mesmo:
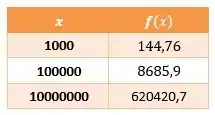
Passo 3
Assim notamos que o valor da função cresce infinitamente enquanto aumentar o , então, o resultado é:
Resposta
Exercícios de Livros Relacionados
Calcule.g) underset(x - + oo)(lim) (sqrt(x + sqrt(x)) - sqrt(x - 1))
Ache o limiteunderset(x - - oo)(lim) (3 x + (1)/(x^2))
Ache o limiteunderset(t - + oo)(lim) ((2)/(t^2) - 4 t)
Ache o limiteunderset(x - + oo)(lim) (7 x^2 - 2 x + 1)/(3 x^2 + 8 x + 5)
Ache o limiteunderset(x - - oo)(lim) (6 x - 4)/(3 x + 1)