Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Alô, meu camarada! Prepare-se, pois hoje vamos desbravar juntos os segredos da função e sua janela retangular.
Imagine que a função é um mapa mágico. A janela retangular? Uma lente especial que nos permite ver apenas uma parte desse mapa, como um farol guiando nosso olhar.
Ao usarmos calculadoras ou computadores poderosos, o mapa da função é desenhado dentro de um retângulo, não mostrando tudo de uma vez. Essa área visível é a nossa janela, a tela de observação, o palco onde a função se revela.
Assim como um explorador mapeia um território passo a passo, a máquina faz o mesmo com a função. Ela define pontos para diferentes valores de , como se estivesse plantando bandeiras ao longo do caminho. Esses pontos, unidos, formam o gráfico da função dentro da nossa janela.
Então, a chave para dominar a janela retangular é escolher os valores de e de forma estratégica, como um diretor de cinema ajustando o foco da câmera. Com a janela certa, podemos revelar os detalhes mais intrigantes da função, desde seus picos e vales até suas curvas e comportamentos inesperados.
Pronto para essa aventura? Vamos juntos explorar os mistérios da função e desvendar os segredos da sua janela retangular!
Então, para construirmos uma janela retangular apropriada, deveremos assim como as calculadoras gráficas, encontrarmos a variação de de até e os valores de de até , e nossa parte visível do gráfico será o retângulo:
Que pode ser vista abaixo como:
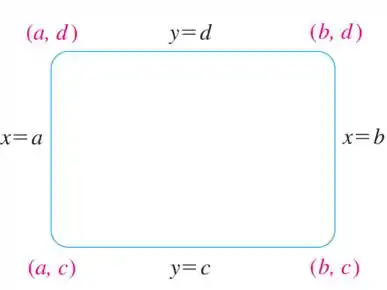
Uma forma de encontrarmos a janela retangular é analisarmos o domínio e a imagem da função. E é isso que iremos fazer aqui.
Passo 2
Vamos então primeiro analisar o domínio da função
Veja que por termos uma raiz, a condição para encontrarmos o domínio é:
Sendo assim, o domínio da função é:
Então temos o nosso primeiro ponto de partida para encontrarmos a janela retangular, pois deveremos partir de e poderemos testar outros valores para o limitante superior. Isso conta da imagem da função.
Veja que a imagem de é
Pois por conta da raiz não temos valores negativos na imagem, e a partir de aceitamos qualquer valor.
Passo 3
Então pelo que foi encontrado, um intervalo inicial interessante para visualizarmos nosso gráfico é perto de e perto de .
Vamos então com o auxilio do GeoGebra gerar o gráfico para diferentes intervalos limitantes superiores como mostrado na figura do passo 1.
Para o retângulo:
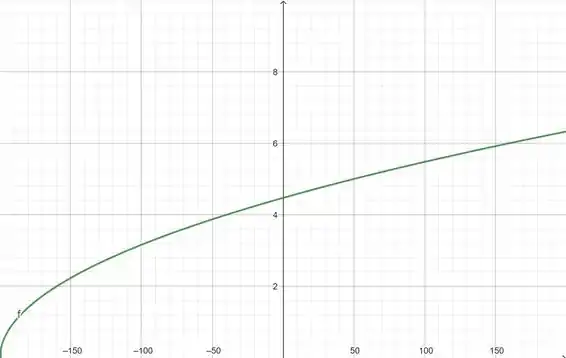
Agora vamos aumentar a visualização para
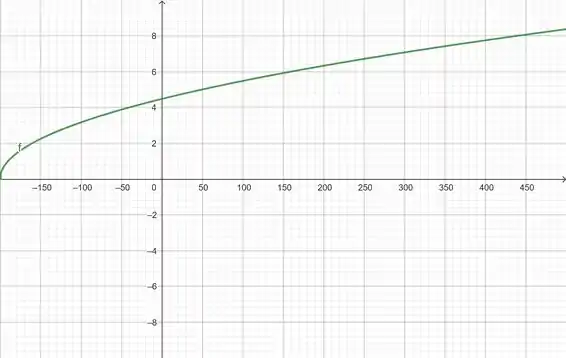
Agora vamos aumentar a visualização para
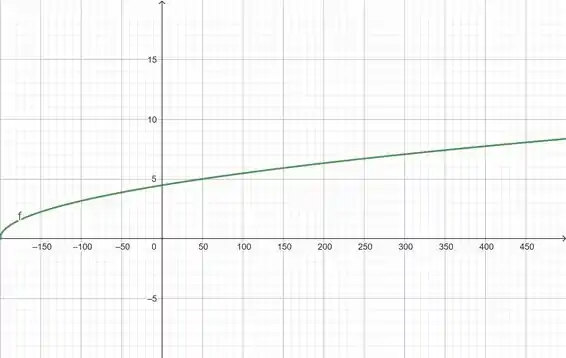
Veja que o retângulo:
Consegue nos mostrar bem o comportamento do gráfico da função, sendo assim ele será o escolhido.