Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 5
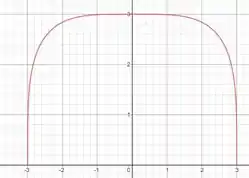
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é determinar uma janela que seja apropriada para esboçar a função e esboçar o gráfico nessa janela.
Parece complicado?
Para determinar a janela da função podemos usar o domínio e a imagem da função a nosso favor. Assim podemos nos situar onde a função é definida.
Caso a gente escolha uma janela equivocada, podemos ter dificuldades em observar o comportamento da função.
Veja só!
Passo 2
A função é dada por
Vamos começar determinando o domínio da função...
O domínio de uma função nada mais é do que os possíveis valores que a sua variavel pode assumir para que a função seja definida.
Nesse caso, temos uma raiz de indece par, então o conteúdo dela deve ser maior ou igual a já que raiz de numero negativo não existe...
Portanto, temos que
A partir dessa inequações, podemos que tem que estar no intervalo
A função é definida apenas nesse intervalo em . Logo as coordenadas em da nossa janela por ser
Tranquilo até aqui?
Passo 3
Agora vamos determinar a imagem da função para determinar o intervalo em da janela.
pode assumir um numero bem finito de valores, dessa forma, vamos analisar algumas coisas...
Perceba que carrega um numero negativo... portanto quanto maior , menor é a imagem da função.
Com isso podemos afirmar que o maior ponto da função acontece em
E conforme aumenta, diminui, logo, em , temos
Descobrimos qual é o maior ponto e tambem o menor ponto da imagem da função, portando um bom intervalo em da nossa janela pode ser descrito como
Show?
Passo 4
Agora só nos resta esboçar o gráfico da função na janela que definimos e .
Como vimos no passo anterior, uma característica da função, é ter seu ponto máximo em , quando e seus pontos mínimos em e , quando .
Com as curvas características de uma raiz, podemos esboçar o gráfico como
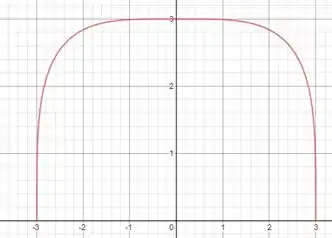
Prontinho! Entendeu tudo? Responde Aí!
Resposta
e
