Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 14
Determine uma janela retangular apropriada para a função dada e use-a para fazer o gráfico da função.
Passo 1
Eaee, belezinha?? Bom... a questão pede para determinarmos uma janela retangular adequada para a seguinte função:
Em seguida, devemos esboçar o gráfico nessa janela.
Lembre-se que janela retangular adequada para uma função em geral refere-se a uma região retangular no plano que é suficientemente grande para conter a curva da função.
Mas não é tão grande a ponto de incluir uma área desnecessária.
Para isso, uma ideia é plotarmos o gráfico e analisar como podemos resumir ele, belezinha??
Bora lá!! 😉
Passo 2
Plotando o gráfico, temos:
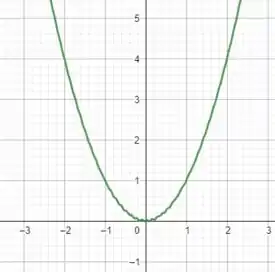
Perceba que trata-se de uma parábola com uma pequena oscilação próximo da origem!!
Perceba que isso faz sentido pois a função tem um e um seno!!
Mas e aí? Qual a janela retangular mais interessante para esse caso?
Bom... Já sabemos que quanto mais se distancia da origem, mais ele irá se aproximar de uma função do tipo , o que nos torna desnecessário analisar o gráfico para verificar valores de grandes em uma parábola.
E, quanto mais próximo da origem, maior é a oscilação.
Além disso, não precisaremos de termos negativos do eixo :
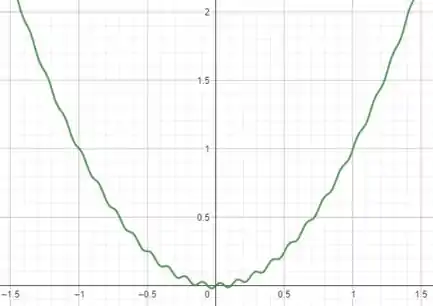
Passo 3
Então uma janelta retangular adequada é uma que mostre essa oscilação e o seu decaimento, ou seja, a janela retangular :
Resposta
