Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 82
Esboce algumas curvas para mostrar que as três partes do teste da derivada primeira (Teorema ) podem ser falsas, sem a hipótese de que seja contínua em .
Passo 1
Vamos lá, temos que o Teste da Derivada Primeira nos diz que:
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um máximo relativo em .
Se em um intervalo aberto imediatamente à esquerda de e em um intervalo aberto imediatamente à direita de , então tem um mínimo relativo em .
E se tiver o mesmo sinal tanto em um intervalo aberto imediatamente à esquerda de quanto em um intervalo aberto imediatamente à direita de , então não tem extremo relativo em .
Passo 2
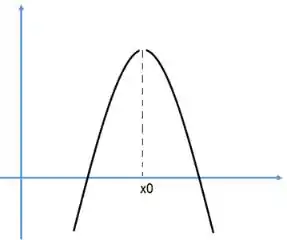
Temos que quando para e para de acordo com o Teorema nós diríamos que o ponto seria um ponto de máximo, mas isso não seria verdade de a função não é contínua em . Como podemos ver no gráfico abaixo:
Passo 3
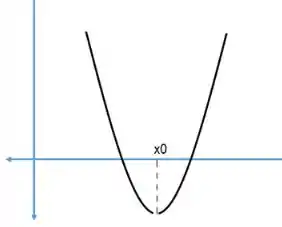
E da mesma forma quando para e para de acordo com o Teorema nós diríamos que o ponto seria um ponto de mínimo, mas isso não seria verdade de a função não é contínua em .
Passo 4
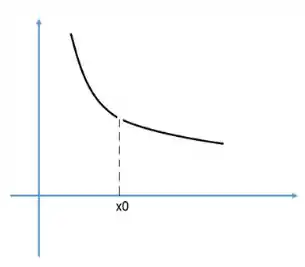
Por último, se tem o mesmo sinal em um intervalo aberto , então não tem extremo relativo em . Entretanto isso é falso se a função não é contínua em .
Resposta
Ei, a resposta está no passo a passo :)