Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 18
Mostre que é uma assíntota curvilínea do gráfico de . Esboce o gráfico de , mostrando esse comportamento assintótico.
Passo 1
Vamos analisar a função, como o numerador tem grau maior do que o denominador podemos reescrever realizando a divisão:
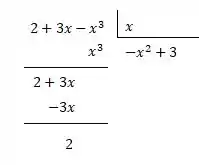
Temos assim:
Assim .
Passo 2
Agora vamos determinar o comportamento no infinito do gráfico, temos que a parcela tende a quando ou , assim:
Quando ou .
Geometricamente isso significa que o gráfico de vai ficando cada vez mais próximo da reta quando ou , e essa reta é denominada assíntota oblíqua ou inclinada de .
Passo 3
E aqui temos o gráfico da função, com a reta pontilhada de azul:
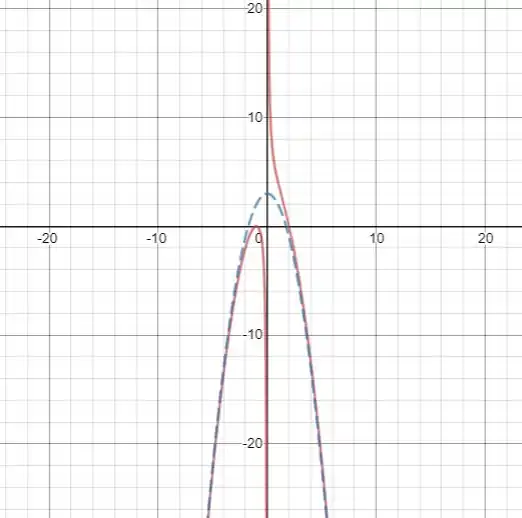
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais, verticais, obliquas e curvilíneas e dê suas equações. I
Mostre que y = x + 3 é uma assíntota oblíqua do gráfico de f x = x 2 x - 3 . Esboce o gráfico de y = f x , mostrando esse comportamento assintótico.
Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais, verticais, oblíquas e curvilíneas e dê suas equações. I
Esboce um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais, verticais, oblíquas e curvilíneas e dê suas equações. I