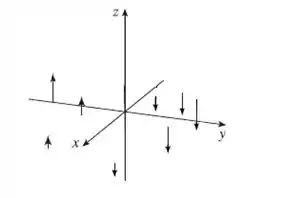
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
Oi galera, tudo bem? Primeiro vamos analisar o módulo desse vetor. A sua norma é:
Esse campo vetorial depende da região de . Quanto mais longe da origem, maior o tamanho do vetor.
Em todo espaço vetorial, eles apontam ao longo do eixo , independente do ponto do espaço.
Para a região de positivo, os vetores apontam para baixo. E na região de , para cima.
Passo 2
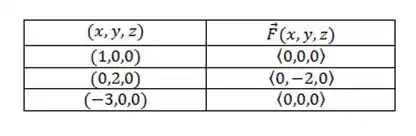
Vamos fazer uma tabela com alguns valores de e os respectivos vetores nesses pontos:
Saca só como fica esse campo vetorial em um sistema cartesiano:
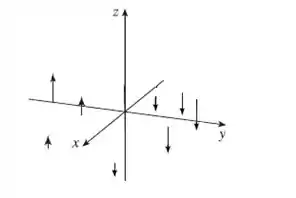
Resposta