Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 33
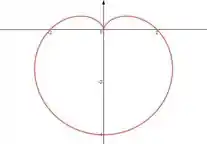
Esboce a curva com a equação dada.
Passo 1
Fala ai pessoal! Tudo de boa?
Para esboçar a curva com a equação polar para , que tal seguir os seguintes procedimentos. siga estes passos:
- Identificar o Comportamento de
- Traçar os Pontos-Chave
- Esboçar a Curva
- Indicar carateríticas da curva.
Eai, entendeu? Vamos começar!!
Passo 2
O que a equação representa?
Nas equações polares o representa a disância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido, então vamos na raça.
Passo 3
Primeiramente calculamos valores de para alguns valores de :
Vamos calcular para e
Para
Para
Para
Para
Para
Passo 4
Vamos verificar agora o comportamento de em relação a :
A equação representa um círculo com centro em .
Quando , , então , ou seja, o ponto mais próximo da origem é .
À medida que aumenta até , aumenta até , então diminui até , alcançando o ponto mais distante .
Passo 5
Desta forma o nosso gráfico começa com uma angulação de à uma distancia de da origem e até ou essa distancia diminui até , até ela aumenta de novo ate , até ela aumenta mais ainda para e diminui até retornar à ou para .
Desenhando no plano fica algo assim:
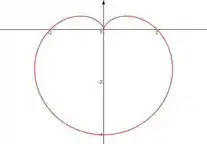
Resposta
