Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 3

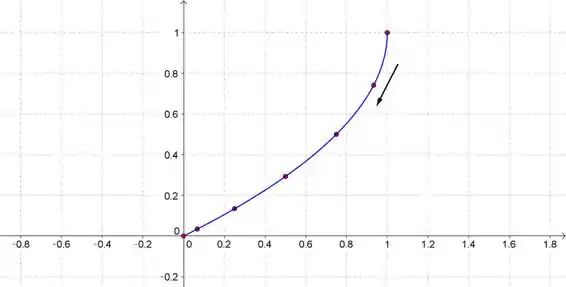
Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva �� traçada quando t aumenta

Passo 1

Oie, meu querido estudante. Vou te ajudar a resolver essa atividade aqui.

Essa é um exercício que te ajuda a criar gráficos. Algo muito importante, principalmente quando formos avançando e chegando por exemplo em cálculo 3.

A gente tem a curva parametrizada:

Vamos fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico. Vamos utilizar o GeoGebra para plotarmos os pontos e consequentemente o gráfico, mas sinta-se a vontade para utilizar qualquer outro software para realizar essa etapa.

Passo 2

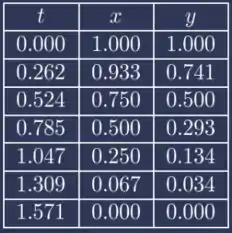
Então, criando nossa tabela, temos:

Beleza, tendo esses pontos, já podemos criar os gráficos. Plotando um ponto de cada vez, temos o seguinte gráfico abaixo:

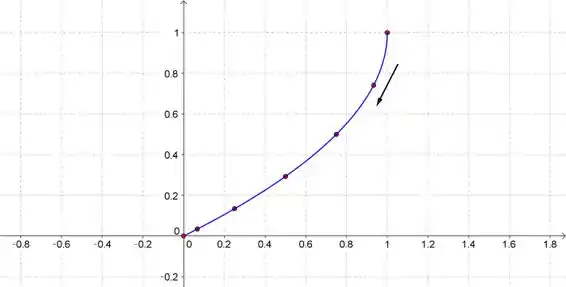
Veja que nosso gráfico é aproximado, quanto mais pontos a gente colocar no gráfico mais preciso ele será.

Veja que pela tabela, quando os valores de aumentam, os valores de e diminuem. A seta ajuda a visualizar o que acontece.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma família de curvas é dada pelas equações r = 1 + c sen ⁡ n θ Onde c é um número real e n é um número inteiro positivo. Como o gráfico muda quando n aumenta? Como ele muda quando c varia? Ilustre tr

Uma família de curvas tem equações polares r = 1 - acos ⁡ θ 1 + a cos ⁡ θ Investigue como o gráfico muda quando a varia. Em particular, você deveria identificar, plotando a curva com uma ferramenta gr

O astrônomo Giovanni Cassini (1965-1712) estudou a família de curvas com equações polares r 4 - 2 c 2 r 2 cos ⁡ 2 θ + c 4 - a 4 = 0 Para as quais a e c são números reais positivos. Essas curvas são ch

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta.3. x = 5s e nt , y = t 2 ,- π ≤ t ≤ π

Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta. x = e - t + t , y = e t - t ,- 2 ≤ t ≤ 2