- Elimine o parâmetro para encontrar uma equação cartesiana da curva.
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Olá, meu amigo. Temos aqui trabalhos a fazer.
Deveremos retirar a parametrização da nossa curva:
Isso é, deveremos colocar a equação em coordenadas cartesianas.
E para isso iremos isolar um termo em comum em uma equação, e substituir em outra. Para fazer o gráfico, a gente vai criar uma tabela com os valores de , e os respectivos valores de e Após isso, poderemos colocar esses pontos num gráfico e assim termos a nossa curva.
Passo 2
Temos que:
Podemos escrever como:
Então:
Substituindo:
Então, nosso gráfico, vamos a criação da nossa tabela:

Veja que e sempre será maior que zero.
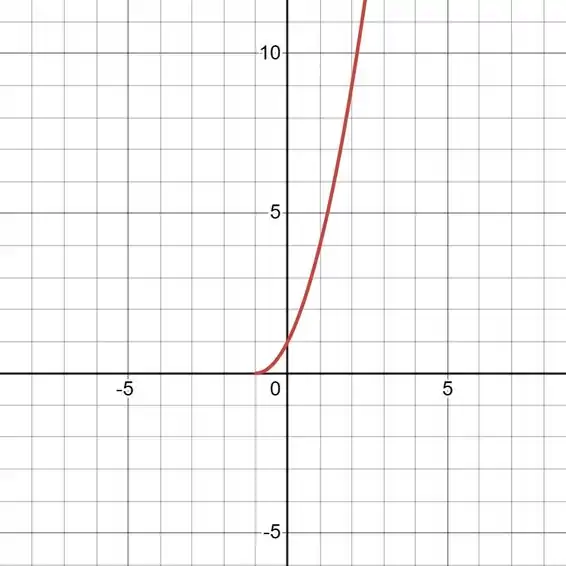
Vamos então ao nosso gráfico:
![]()
Veja que a medida que cresce, tanto quando crescem também.
Resposta