Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 15
A ) Elimine os parâmetros para encontrar uma equação cartesiana da curva
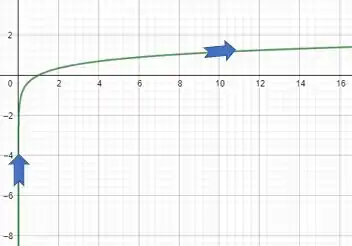
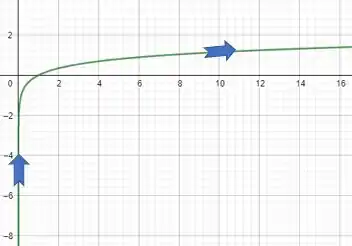
B ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta
Passo 1
Olá, meu amigo. Temos aqui trabalhos a fazer.
Deveremos retirar a parametrização da nossa curva:
Isso é, deveremos colocar a equação em coordenadas cartesianas.
E para isso iremos isolar um termo em comum em uma equação, e substituir em outra.
Para o gráfico, vamos fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico. Assim a gente tem o esboço do mesmo e a direção da curva quando o parâmetro cresce.
Passo 2
Agora vamos voltar do mundo paramétrico para o cartesiano. A melhor solução para isso é isolar alguma das variáveis e substituir na outra.
Matematicamente será bem tranquilo, mas você vai precisar de uma intuição para qual a melhor variável para isolar seja ela ou . Vamos cair dentro então:
Aqui o mais fácil para isolar é o , então vamos nele:
Vamos substituir em :
Então a gente tem já a nossa curva em coordenadas cartesianas. Vamos partir para a criação do esboço do gráfico.
Passo 3
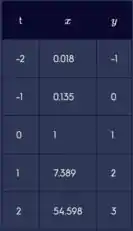
A gente vai criar uma tabela, pois é assim que provavelmente você faria se estivesse na prova e precisasse de um esboço:
Aqui a gente vai utilizar o GeoGebra para traçar o gráfico, melhor do que a gente colocar pontinhos por pontinhos no papel:
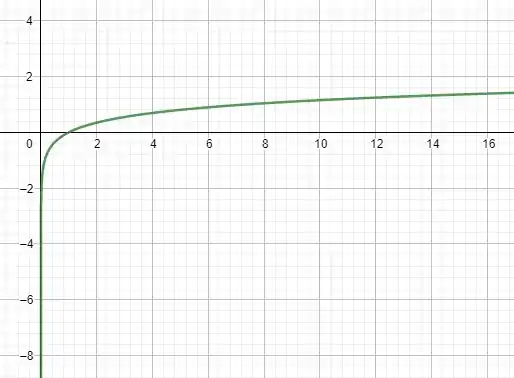
Para orientarmos esse gráfico não temos nenhum truque magico, temos que analisar a tabela mesmo. Conforme cresce, também cresce. Então isso nos dá que a direção é:
