Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 20
Descreva o movimento de uma partícula com posição quando varia no intervalo dado.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade juntos.
Aqui a gente vai descrever o movimento da partícula:
Conforme o seu varia. Para isso, vamos fazer uma tabela com diferentes valores para e iremos a partir disso encontrar os respectivos valores de e de .
Depois disso iremos utilizar o GeoGebra para plotar esses pontos e entendermos o comportamento da figura.
Passo 2
Então temos a tabela:
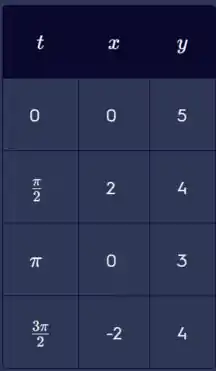
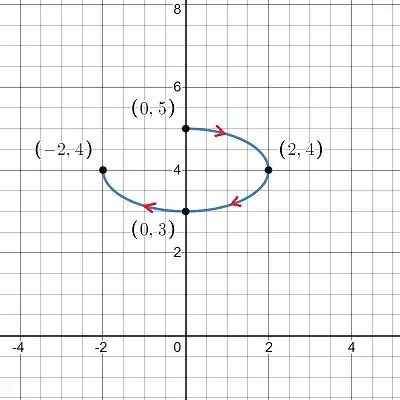
Vamos montar o gráfico colocando os pontos e traçando o caminho:
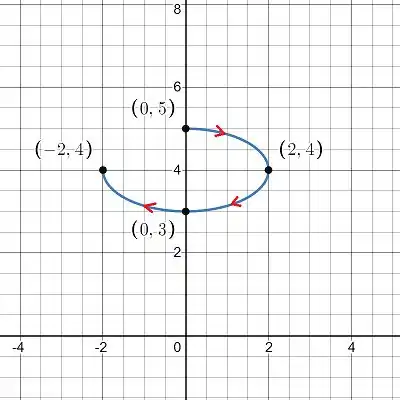
Para conferir nosso resultado, vamos dar uma olhada na curva e coloca-la em coordenadas cartesianas, assim poderemos ver se encontramos uma equação conhecida e assim de fato termos a figura que esboçamos.
Organizando um pouquinho para isolarmos o parâmetro, ficamos com:
Quando a gente vê um seno e um cosseno dá uma vontade de elevar ao quadrado e igualar a 1, né? Podemos fazer isso:
Substituindo pelos valores que temos no enunciado ficamos com isso aqui:
Podemos perceber, por essa equação movimento da partícula ocorre em uma elipse centrada em . Como tínhamos feito no nosso esboço. Temos então duas formas de encontrar o movimento de uma partícula.
Realizando os esboços do seu gráfico a partir de uma tabela, ou encontrando sua equação em coordenadas cartesianas.
Resposta
