Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 37
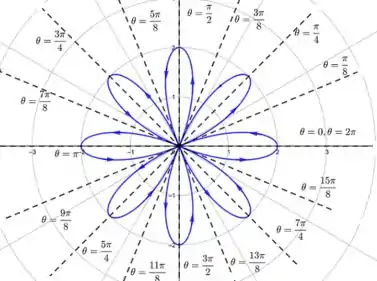
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Então com auxílio de um software gráfico podemos plotar essa função dessa forma e obtermos uma figura oscilatória e limitada por conta do comportamento da função cosseno.
Passo 2
Utilizando o um software gráfico, podemos plotar a figura do gráfico:
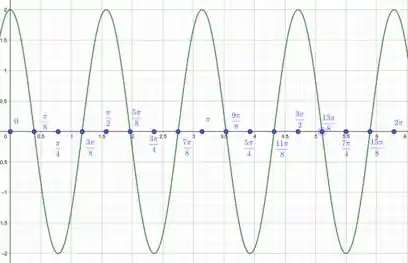
Essa imagem mostra em coordenadas cartesianas, onde o eixo representa e o eixo representa .
Passo 3
Observamos na imagem anterior que quando aumenta de a diminui de para . Vamos esboçar essa parte da curva.
Então, quando aumenta de para vai de para . Agora vamos esboçar essa parte da curva.
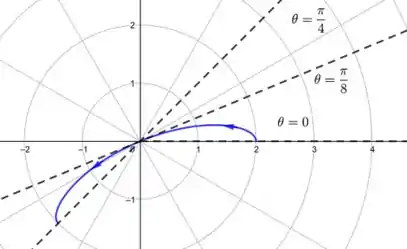
Continuando esse processo até que alcance , obteremos nossa curva. Após , voltaríamos a traçar nossa curva.
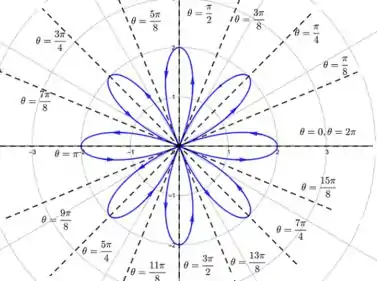
Resposta
