Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 38
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Primeiro, faça um gráfico cartesiano com no eixo horizontal e no eixo vertical. Esta é a transformação de com amplitude , então . Pegue o na frente de e dívida por ele para obter o período:
Para fazer um esboço aproximado, é tudo o que precisamos saber, pois estamos familiarizados com o gráfico de . Comece no valor médio , suba até o valor máximo , volte para cima e cruze o eixo em , depois volte a subir até em , repita algumas vezes.
Para o gráfico no plano polar, nós iremos criar uma tabela com os valores de raio zero e iremos relacionar com o gráfico do plano cartesiano, assim iremos correlacionar a oscilação existente da figura em ambos os planos e poderemos criar o gráfico da figura corretamente no plano polar.
É mais fácil fazer do que falar, mas lembre que estamos trabalhando com uma curva limitada e oscilatória dada a natureza da função seno.
Passo 2
Temos então o grafico no plano cartesiano:
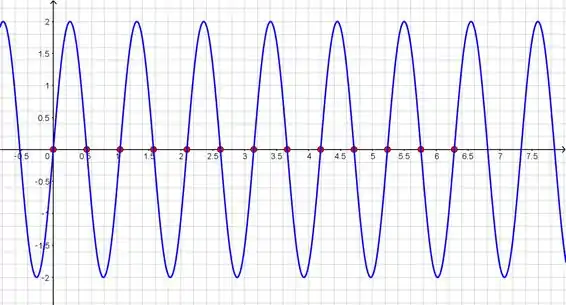
Passo 3
Veja abaixo a tabela de zeros da nossa curva:
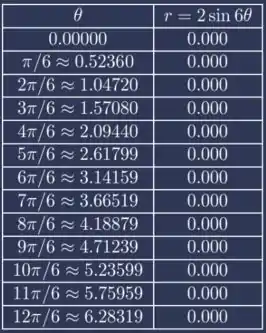
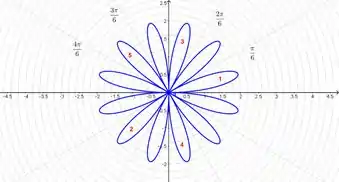
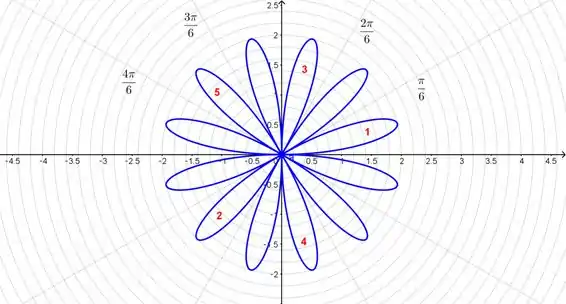
Do gráfico cartesiano nós temos que a primeira pétala é desenhada no sentido positivo de . De até nós desenhamos a pétala de até então nós voltamos para .
A próxima pétala é quando , de até .
As primeiras 5 pétalas são numeradas na ordem em que são desenhadas enquanto vai de a e alterna entre positivo e negativo. Siga o padrão para desenhar o restante. Além disso, algumas das linhas de ângulo estão marcadas.
Resposta
