Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 40
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
Já para encontrarmos os gráficos no plano polar e no plano cartesiano nós iremos criar uma tabela com diversos pontos para e seu respectivo valor de .
Uma ajuda importante é saber que a nossa figura faz parte da família de limaçons, que possuem equação:
Para , há um laço que diminui de tamanho à medida que diminui. Quando , o laço desaparece e a curva se torna a cardioide.
Para entre e , o cume da cardioide é suavizado e se torna um covinha.
Quando diminui de para , o limaçon assume a forma de um oval. Este oval torna-se mais circular à medida que se aproxima de e, quando , a curva é apenas o círculo .
Passo 2
Então, temos nossa tabela:
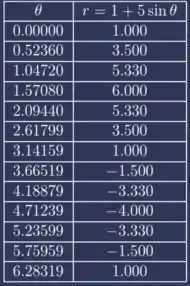
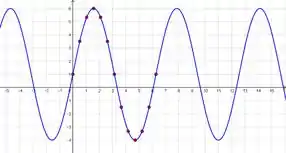
Agora iremos colocar esses pontos no plano cartesiano:
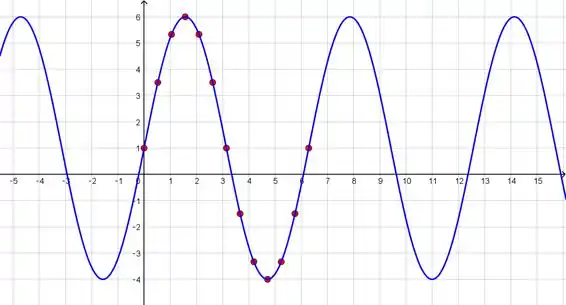
Veja que o que temos aqui é a transformação do gráfico da função:
Com agora a amplitude de e uma elevação de . Temos também que o período da função é de
Passo 3
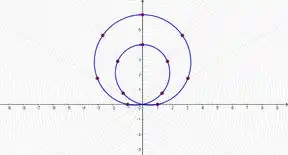
Com essa mesma tabela, porém agora no plano polar, temos o seguinte gráfico para a função:
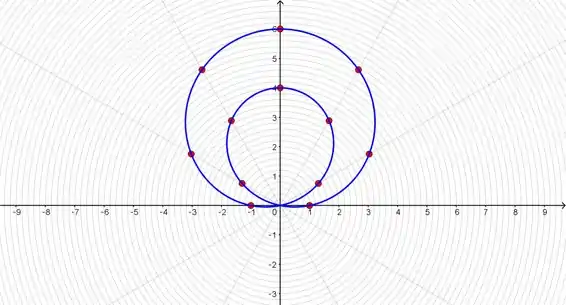
Temos então que nossa curva faz parte dos limaçons
Onde . Para casos em que temos acontece a criação do loop interno que vemos na nossa figura.
Resposta
