Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 34
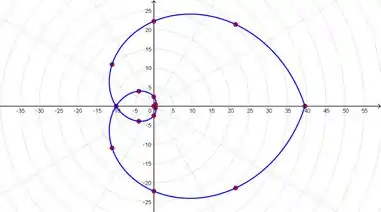
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Então meu querido e amado estudante, pronto para mais uma resolução?
Aqui a gente precisa esboçar a curva dada, porém essa curva é dada em coordenadas polares, então o que a questão quer que a gente faça é tratar ela como se ela fosse em coordenadas cartesianas.
É como se a função fosse na verdade:
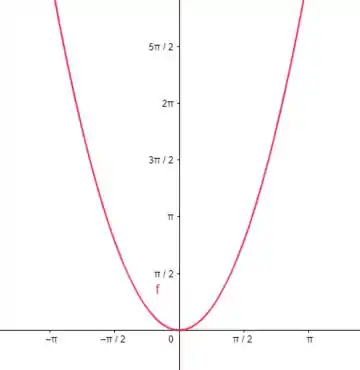
O gráfico vai ser uma parábola.
Agora para o esboço do gráfico em coordenadas polares, a gente vai criar uma tabela, com os valores para e para , e assim teremos diversos pontos a serem plotados em um gráfico. Assim a gente vai obter esse esboço que a gente quer.
Passo 2
Gerando o gráfico da parábola:
Passo 3
A nossa tabela fica:
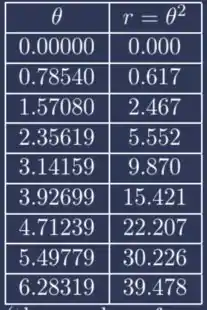
Plotando esses pontos num software gráfico, a gente pode plotar os pontos polares :
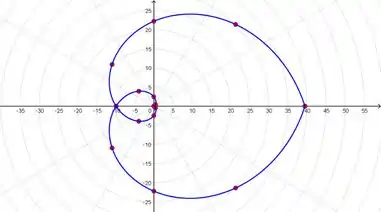
Então é isso, você pode, a fim de obter maior precisão, criar uma tabela com mais valores, mas estamos aqui apenas falando de um esboço, então fique a vontade para fazer da forma que achar melhor.
Veja que a depender de qual plano estamos trabalhando, a figura terá diferentes formas, por isso é importante colocar cada tipo de coordenada em seu plano correto.
Resposta
