Marque os pontos cujas coordenadas polares são dadas. A seguir, encontre dois outros pares de coordenadas polares desse ponto, um com e o outro com :
Passo 1
- Vamos lá, marcando o primeiro ponto. É raio 2 e ângulo .
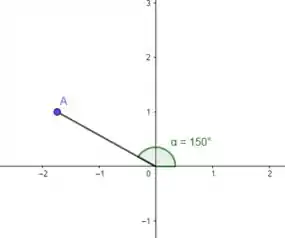
Os pontos correspondentes são com raio positivo:
(o ponto vai tá do mesmo lado)
Agora para o raio negativo, é só a gente pegar o ângulo oposto. Vamos inverter o raio e pegar o ângulo oposto. Fica:
Passo 2
Pro item b) agora, temos raio 1 e ângulo
Esse ângulo tá negativo, então a gente percorre no sentido horário:
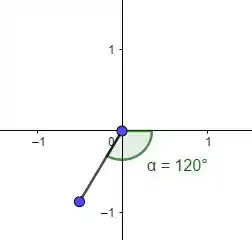
Beleza, com raio positivo a gente pega um ponto do mesmo lado:
Com raio negativo a gente pega o ponto oposto:
Passo 3
No item agora:
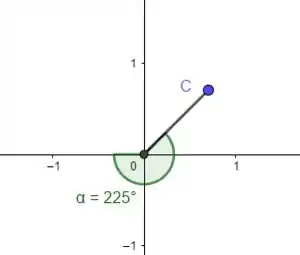
Pra raio positivo, a gente tem que pegar um correspondente do mesmo lado:
Nesse caso podemos pegar:
Com raio negativo a gente pega o oposto:
Prontinho!
Resposta
Ei, a resposta está no passo a passo :)