Associe cada equação a seu gráfico. Explique sua escolha. (Não use computador ou calculadora gráfica)
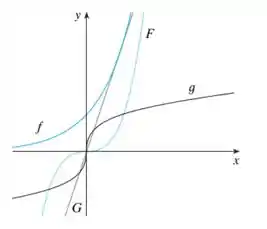
Passo 1
Opa, bora lá! Temos as seguintes curvas:
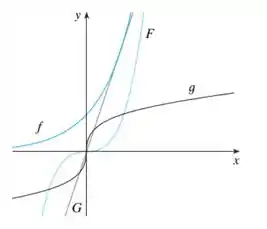
Temos que dizer que curva pertence a que função entre essas daqui:
Pra isso a gente tem que resgatar os nossos conhecimentos sobre funções! Vamos lá!
Mas primeiro, vamos analisar cada uma dessas funções pra entender o comportamento delas e depois a gente identifica cada uma no gráfico.
Passo 2
Essa função tem a forma geral , ela é uma função de primeiro grau e portanto uma reta. Como o coeficiente linear é 0, ela passa pela origem.
Nossa única reta é a função .
Passo 3
Essa função é da forma , é uma função exponencial. Isso significa que ela vai ser sempre positiva. Ela vai crescer MUITOOO quando cresce e vai ficar muito muito pequena quando tem valores negativos, mas ainda positiva.
A função que apresenta esse comportamento é a
Passo 4
Essa é um potência ou uma função polinomial de grau 3. Ela vai crescer bastante quando cresce e decresce bastante quando decresce. Quando , ela também é positiva e quando , ela também é negativa.
A função que apresenta esse comportamento é a
Passo 5
E essa última é uma função raiz. Ela pode assumir valores negativos, quando for negativo. E ela não tem inclinação tão grande assim, porque a função raiz tem um expoente fracionário
Como essa é um pouco mais incomum, aqui em baixo ta o gráfico de funções raízes de índice par e índice ímpar, dá uma olhada:
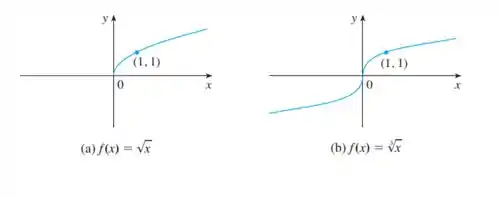
Então o que temos mais parecido com isso é a função . Mas na verdade, já sabíamos disso por eliminação.
Prontinho!
Resposta
corresponde à
corresponde ��
corresponde à
corresponde à