Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 7
(a) Esboce o gráfico da curva plana com equação vetorial dada.
(b) Determine r’(t).
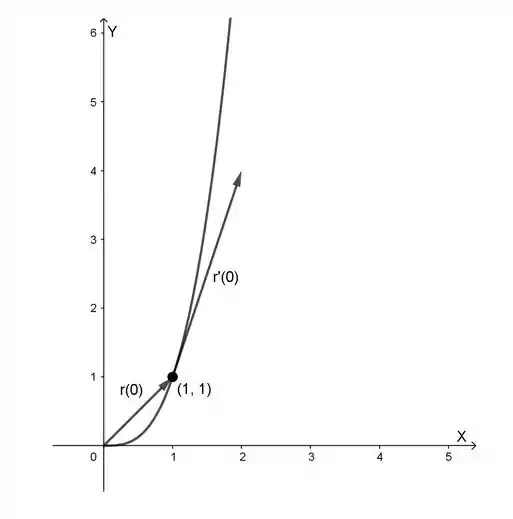
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Passo 1
Olá, meu brother. Vamos resolver mais uma atividade? Veja bem.
Deveremos esboçar essa figura, para isso iremos utilizar um software gráfico. Mas antes, iremos colocar nossa curva em coordenadas cartesianas, isso irá facilitar para a gente. Para colocarmos em coordenadas cartesianas nós deveremos correlacionar as funções e de .
Para derivarmos a função é só a gente derivar cada termo do nosso vetor.
Passo 2
- Temos então:
- Determinamos derivando as componentes de .
Ou
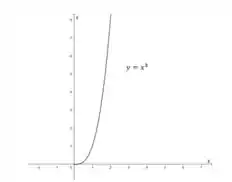
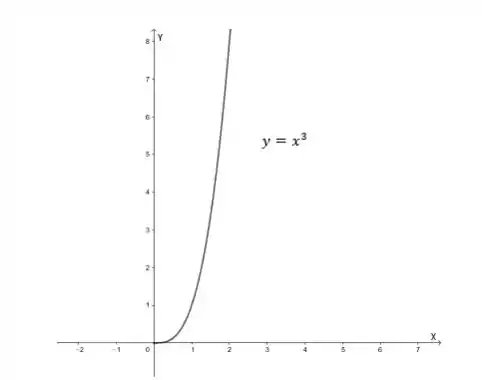
Com base nas equações paramétricas percebemos que
Essa equação representa uma curva cúbica normalmente conhecida nos estudos de funções.
Como a função é positiva para todo , observa-se que e . Portanto o gráfico da curva é dado pelos valores positivos da função .
Passo 2
Derivando:
Veja que tivemos que utilizar a regra da cadeia para derivar:
Pois aqui estamos com uma composição de funções.
Passo 3
O vetor posição em é
Por outro lado, o vetor tangente em , tem origem no ponto e é dado por:
Com base nos resultados obtidos podemos representar esses vetores conforme mostrado na figura abaixo:
