Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.3 - Ex. 37
Trace a curva espacial e sua função curvatura . Comente como a curvatura reflete a forma da curva.
Passo 1
Fala ai pessoal!
Tranquilo? Para conseguirmos traçar a função , temos primeiro que encontrá-la. E como podemos fazer isso? Que tal seguirmos alguns passos?
1 – Determinar as derivadas da função vetorial
2 – Calcular o produto vetorial entre a derivadas primeira e a derivada segunda
3 – Verificar o módulo
4 – Calcular a função da curvatura através da fórmula 9
5 – Análise para construção do gráfico.
Vamos começar!
Passo 2
Vamos lembrar que a função curvatura é dada por
E que o produto vetorial é dito
Passo 3
Calculando
Calculando
Passo 4
Dada a função , podemos dizer que
Simplificando cada termo:
Passo 5
Calculando
Simplificando
Passo 6
Calculando agora
Simplificando cada termo
Passo 7
Cálculo de
Passo 8
A curvatura quantifica como a curva muda sua direção em diferentes pontos. Em regiões onde é maior, a curva está mudando de direção mais rapidamente, indicando maior curvatura ou "torção". Em regiões onde é menor, a curva é mais suave e se aproxima de uma linha reta.
Primeiramente traçamos o gráfico de
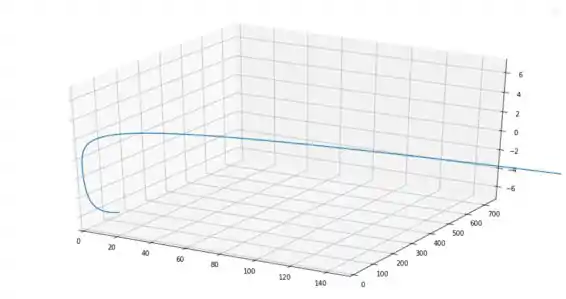
Passo 9
Em seguida temos
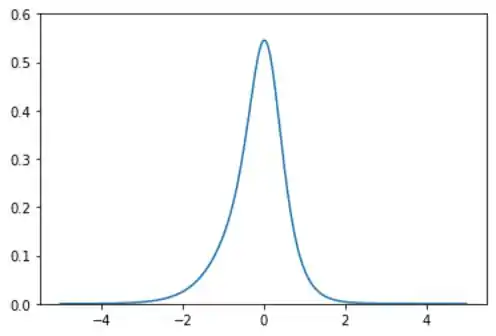
Para a curva , a função curvatura refletirá as variações de curvatura ao longo do intervalo . Por exemplo, perto de , onde as derivadas são mais simples, a curvatura pode ser menor, enquanto em valores extremos de , a curva pode ter maiores mudanças de direção, resultando em maior curvatura.
Resposta
