Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 10
Esboce a região no plano que consiste em pontos cujas coordenadas polares satisfazem as condições dadas:
Passo 1
Falaee, tudo certinho?? Bom... nessa questão a gente quer esboçar a seguinte inequação polar:
No intervalo .
Mas e aí?? Como fazemos isso??
Bom... aqui a nossa solução é interpretarmos o que nos foi dado. Quer saber como?? Bora lá!!
Passo 2
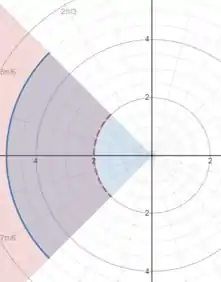
Vamos interpretar a nossa inequação:
Em termos mais simples, temos que a região do nosso plano corresponde a tuuudo que tiver entre e .
Se fosse só isso, o nosso esboço seria todo o plano real entre esses valores... seria tipo um disco de raio menor e raio maior .
Maaaas, o enunciado restringiu ao intervalo:
Assim, selecionando os ângulos e , temos:
Resposta
Exercícios de Livros Relacionados
53.Prove o Teorema 10.6.2.
Nos exercícios 55 e 56, o gráfico da equação dada intercepta a si mesmo. Ache os pontos nos quais isso ocorre.56. r = 1 + 2 c o s 2 θ
54.Prove o Teorema 10.6.3.
Nos exercícios 55 e 56, o gráfico da equação dada intercepta a si mesmo. Ache os pontos nos quais isso ocorre.55. r = s e n 3 2 θ
Nos exercicos de 37 a 52, ache os pontos de intersecção dos gráficos do par de equações dadas. Faça um esboço de cada par de gráfico com o mesmo eixo polar e a mesma origem. r =sen 2 θ r = cos 2 θ