Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 13.3 - Ex. 36
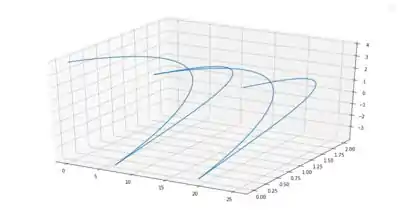
Trace a curva espacial e sua função curvatura . Comente como a curvatura reflete a forma da curva.
Passo 1
Fala ai pessoal!
Tranquilo? Para conseguirmos traçar a função , temos primeiro que encontrá-la. E como podemos fazer isso? Que tal seguirmos alguns passos?
1 – Determinar as derivadas da função vetorial
2 – Calcular o produto vetorial entre a derivadas primeira e a derivada segunda
3 – Verificar o módulo
4 – Calcular a função da curvatura através da fórmula 9
5 – Análise para construção do gráfico.
Vamos começar!
Passo 2
Vamos lembrar que a função curvatura é dada por
Calculando
Calculando
Passo 3
Calculando o produto vetorial
Passo 4
Dada a função , podemos dizer que
Simplificando cada componente
Passo 5
Magnitude de
Usando relações trigonométricas:
Simplificando
Passo 6
Cálculo de
Passo 7
Primeiramente traçamos o gráfico de
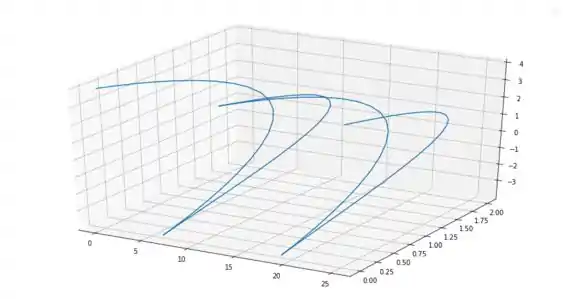
Para a curva , como varia de a , a função curvatura refletirá as variações da curva ao longo desse intervalo, mostrando onde a curva tem mudanças mais acentuadas na direção (onde é maior) e onde a curva é mais suave (onde é menor).
Passo 8
Se observarmos a expressão da curva, percebemos que a presença dos senos e cossenos indica uma oscilação periódica em torno de certas direções, sugerindo que a curva terá segmentos de inflexão e segmentos mais retos, refletindo diretamente na variação da curvatura .
Em seguida temos
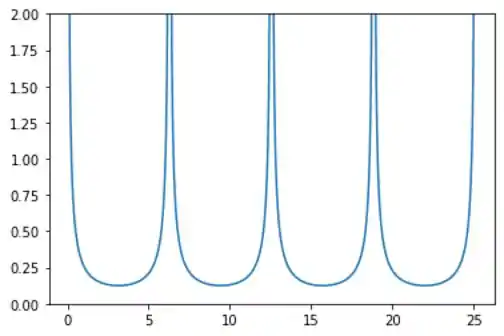
A curvatura nos dá uma medida de quanto a curva está mudando sua direção em um ponto específico. Se for grande, a curva está mudando de direção rapidamente, ou seja, é mais "curvada" nesse ponto. Se for pequena, a curva está mudando de direção lentamente, ou seja, é mais "reta".
Resposta
