Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 26
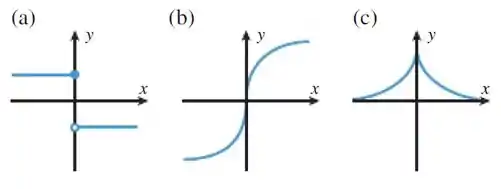
Esboce o gráfico da derivada da função cujo gráfico é dado.
Passo 1
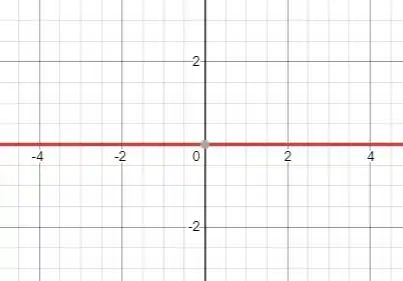
Na função da letra a) em a derivada não é definida, pois a função não é contínua nesse ponto.
Em todos os outros pontos a derivada é igual a zero porque a função é constante, assim abaixo temos o gráfico:
Passo 2
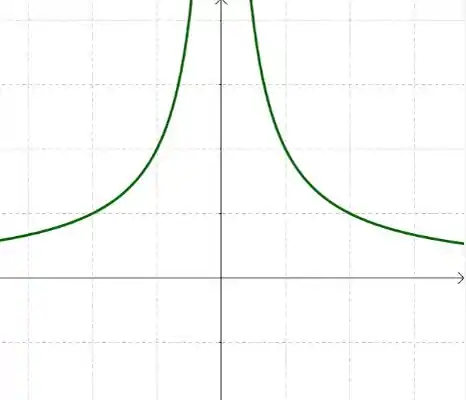
Já a função da letra b) temos inclinações diferentes, uma para e outra para , que estão aumentando em todos os lugares, temos então que a derivada deve ser positiva em todos os lugares. Em a função possui inclinação vertical, que não nos permite possuir uma reta tangente.
Assim podemos esboçar o gráfico da derivada:
Passo 3
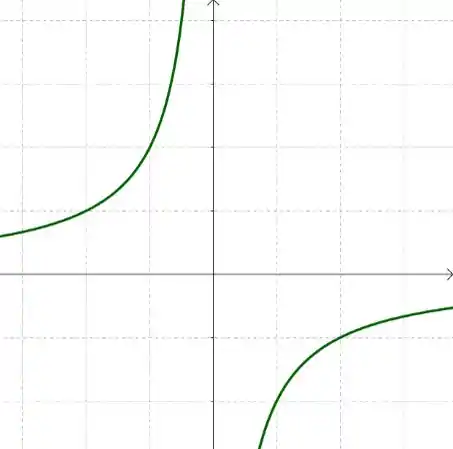
E por último, a função da letra c) está aumentando no lado esquerdo e diminuindo no lado direito, então temos que a derivada deve ser positiva no lado esquerdo e negativa no lado direito. Em a derivada não é definida, pois a função não é contínua nesse ponto, já que alí existe um bico, que não nos permite possuir uma reta tangente.
Vamos então esboçar o gráfico da derivada:
Resposta
Ei, a resposta está no passo a passo :)