Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 1c
Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de
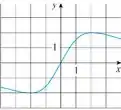
c)
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema foi dado um gráfico de uma função e nosso objetivo é estimar o valor de .
Vish! Parece difícil, né?
Mas, olha só, vou te contar um negócio! a gente vai fazer e você vai mudar de opinião.
Sabemos que o conceito de derivada, é além do limite, né?! A derivada representa o coeficiente angular da reta tangente ao ponto em relação ao eixo .
Resumindo... Vamos ter que desenhar a reta tangente ao ponto e depois tenta estimar o ângulo da reta em relação ao eixo
Mas vamos desenhar primeiro.
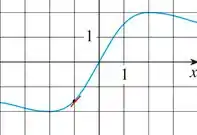
Tranquilo até aqui? 🤔
Passo 2
Temos que, através da nossa tangente encontrar o ângulo formado entre a reta tangente e o eixo no ponto dado. Vamos fazer isso com ajuda da trigonometria, ok?
Vamos dar uma esticadinha na reta tangente e formar uma triangulo retângulo.
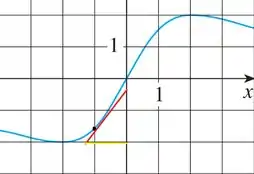
Pronto, temos um triângulo retângulo, percebeu?...como a questão pede uma estimativa, podemos ficar mais tranquilas para achar o ângulo. Então vamos estimar o comprimento da linha amarela e da linha vermelha. Vê se você concorda comigo, beleza?
E,
Vamos usar as relações trigonométricas no triangulo retângulo. Como temos os catetos oposto e adjacente, temos que
Para descobrir o ângulo é só usar a função
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
