Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 46
Mostre que é contínua, mas não diferenciável no ponto dado. Esboce o gráfico de .
Passo 1
- Vamos analisar o gráfico de em :
- Vamos analisar o gráfico de em :
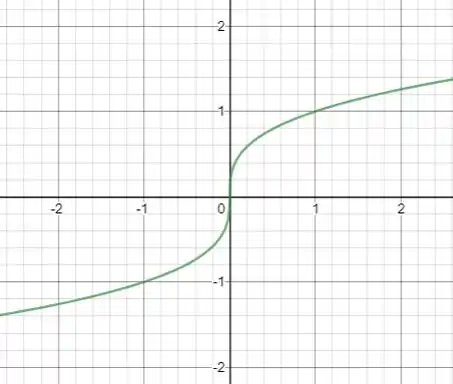
Do gráfico dá pra ver que a função é contínua em , pois existe um valor de .
Mas ela não é diferenciável nesse ponto, porque a reta tangente em é vertical, e não existe uma inclinação para uma reta vertical.
Passo 2
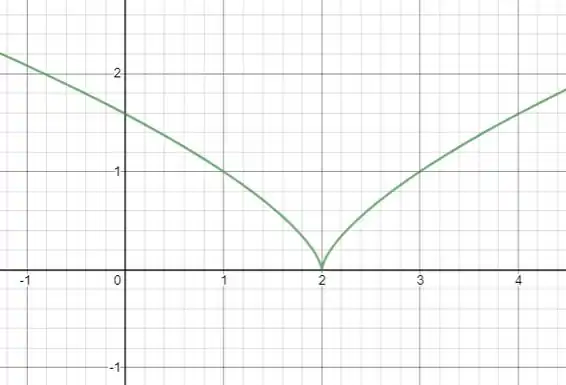
Do gráfico dá pra ver que a função é contínua em , pois existe um valor de .
Mas ela não é diferenciável nesse ponto, porque a reta tangente em não possui uma inclinação, pois nesse ponto temos uma ponta, que não permite obter uma reta tangente.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
26.Encontrar ∆ y - d y das funções dadas.a) y = 3 x 2 - x + 1 b) y = 2 x c) y = x + 1 2 x - 1
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Se uma função f for derivável em x = 0 , então f será continua em x = 0 .
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.Se uma função f for contínua em x = 0 , então f será derivável em x = 0 .
Suponha que uma função f seja diferenciável em x 0 e que f ' x 00 . Prove que existe um intervalo aberto contendo x 0 , tal que, se x 1 e x 2 são dois pontos quaisquer nesse intervalo, com x 1x 0x 2 ,
Suponha que uma função f seja diferenciável em x 0 e defina g x = f m x + b , onde m e b são constantes. Prove que, se x 1 é um ponto tal que m x 1 + b = x 0 , então g x é diferenciável em x 1 e g ' x