Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 16
Esboce o gráfico da equação por translação, reflexão, compressão e alongamento do gráfico de , , , ou de maneira apropriada e, então, use um recurso gráfico para confirmar que seu esboço está correto.
Passo 1
Bem, nessa questão, nós vamos usar os princípios de translação, alongamento, compreensão e reflexão vistos nesse capítulo e que ficaram bem resumidos na tabela 0.2.2, 0.2.3 e 0.2.4.
Basicamente:
Se temos uma função, por exemplo, e somamos uma constante positiva à função, por exemplo , deslocamos o gráfico da função na quantidade equivalente ao valor da constante para cima (no nosso exemplo, deslocaríamos em 1 unidade para cima no eixo ).
Se subtraímos uma constante à função (), deslocamos o gráfico para baixo (no exemplo, seria 1 unidade para baixo no eixo ).
Se somamos uma constante positiva ao (ex.:), deslocamos o gráfico para a esquerda (no exemplo, seria 1 unidade para a esquerda no eixo ).
Se subtraímos uma constante positiva ao (ex.:), deslocamos o gráfico para a direita (no exemplo, seria 1 unidade para a direita no eixo ).
Se multiplicamos a função por uma constante positiva maior que , alongamos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos a função por uma constante positiva entre e , comprimimos o gráfico no eixo vertical por um fator equivalente à constante.
Se multiplicamos por uma constante positiva maior que , comprimimos o gráfico no eixo horizontal por um fator equivalente à constante.
Se multiplicamos por uma constante positiva entre e , alongamos o gráfico no eixo horizontal por um fator equivalente à constante.
Se substituímos por , refletimos o gráfico pelo eixo .
Se multiplicarmos a função por , refletimos o gráfico pelo eixo .
Vamos usar esses conceitos para resolver essa questão!!
Passo 2
Olhando para a função:
Vemos que temos um no denominador, certo? Então, se assemelha mais ao . Mas ainda está estranho, porque estamos somando um número multiplicado por e isso não se encaixa em nada que vimos até agora... Calma! Nada está perdido.
Quando vierem essas coisas fora da caixinha, significa que temos que modificar por manipulações algébricas até se encaixar nos nossos moldes.
O que podemos fazer nessa? Vamos separar essa fração em dois termos:
Simplificando a primeira fração:
Agora sim está nos nossos moldes! Pois temos apenas um termo com .
Passo 3
Vamos identificar as modificações partindo de :
Primeiro, multiplicamos a função por , o que reflete o gráfico de pelo eixo :
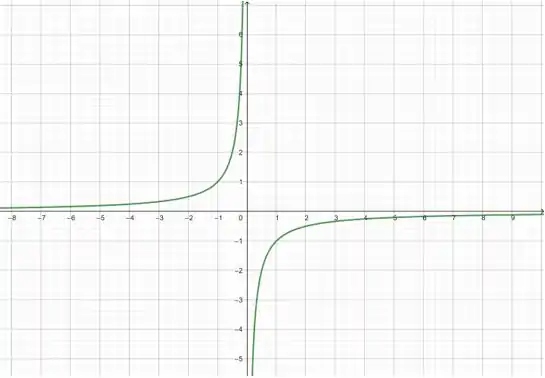
Passo 4
Agora, temos . O próximo passo é somar à função, o que desloca o gráfico em uma unidade para cima:
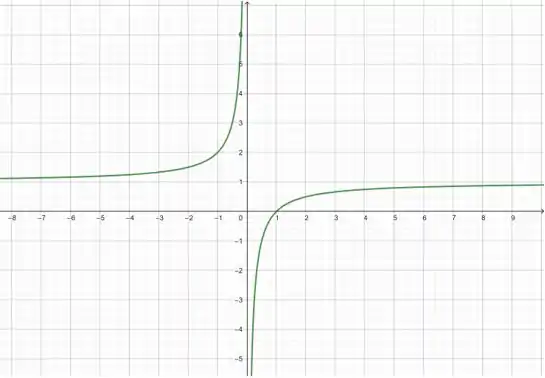
Com isso, chegamos no gráfico de .
Resposta
