Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 8
8. Esboce o gráfico de um exemplo de uma função que satisfaça a todas as condições dadas
é ímpar
Passo 1
Falaeee, belezinha? Bom.. a questão nos dá as seguintes condições abaixo e nos pede para esboçar um gráfico a partir delas:
é ímpar
Dessa forma, temos que analisar as assíntotas horizontais e verticais.
Lembrando que uma assíntota é uma linha que uma curva se aproxima à medida que você segue indefinidamente ao longo da curva.
E aí? Bora lá?
Passo 2
Repare que nesse tipo de questão nós temos diversas soluções. Vou fazer uma, olha só:
Vamos ter duas assíntotas verticais:
e
Pois
Teremos duas assíntotas horizontais:
e
Pois
Como a função é ímpar ainda temos que fazer com que
Passo 3
Dessa forma, com base no que acabamos de ver nos Passo 2, temos o seguinte gráfico:
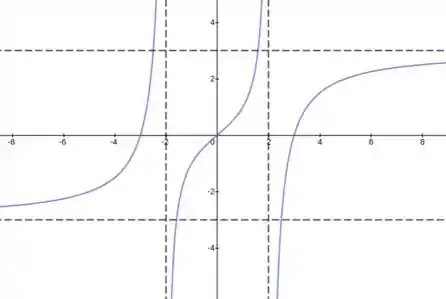
Resposta
Exercícios de Livros Relacionados
Seja f x = b x , em que 0b . Use o princípio da substituição para confirmar o comportamento assintótico dessa função ilustrado na Figura 0.5.1. [Sugestão f x = b x = e ln b x = e ln b x ] .
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas y = f ( x ) e y = g x são assintóticas quando x → + ∞ se: lim x → +
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas y = f ( x ) e y = g x são assintóticas quando x → + ∞ se: lim x → +
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas y = f ( x ) e y = g x são assintóticas quando x → + ∞ se: lim x → +
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas y = f ( x ) e y = g x são assintóticas quando x → + ∞ se: lim x → +