Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 7
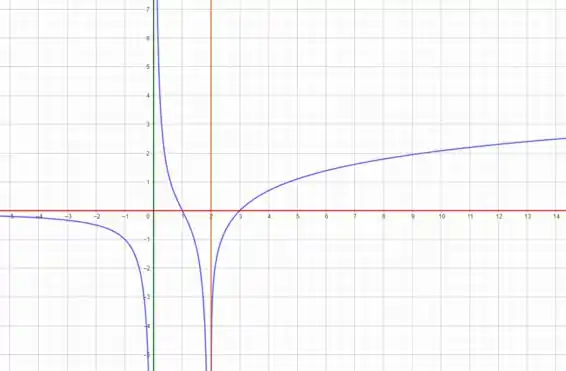
7. Esboce o gráfico de um exemplo de uma função que satisfaça a todas as condições dadas
Passo 1
Fala aí! tudo certinho? 😊
Nesse problema queremos obter um esboço do gráfico da função descrita por umas dadas condições no enunciado.
Nossas condições são as seguintes:
Parece complicado? 👀
Repara que aparece “infinito” em todos os limites que ele deu. Isso já nos induz a pensar em assíntotas horizontais e verticais.
Lembrando das definições de assíntotas horizontais:
- A reta é chamada assíntota horizontal da curva se:
ou
Já para assíntotas verticais:
- A reta é chamada assíntota vertical da curva se:
ou
Passo 2
Foi dito que .
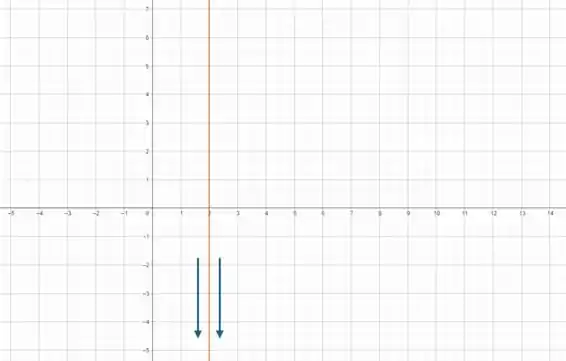
Esse dado nos diz que , ou seja, temos uma assíntota vertical em em que ambos os lados dessa assíntota tendem a .
Traçando a reta (em laranja) e as setinhas indicando que o limite vai pra menos infinito:
Passo 3
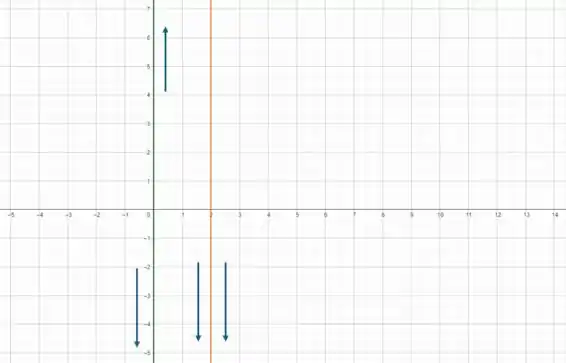
Agora para e temos que em temos outra assíntota vertical, mas dessa vez a função tende a pela direita e pela esquerda.
Traçando a reta em verde e as setinhas indicando que vai pra mais infinito pela direita e pra menos infinito pela esquerda:
Passo 4
E por fim, foi dito que e ou seja, se tende a quando tende a e tende a quando tende a .
Traçando a reta (em vermelho) e as setinhas indicando que quando tende a menos infinito, o limite é igual a zero e que quando tende a mais infinito, o limite é mais infinito:
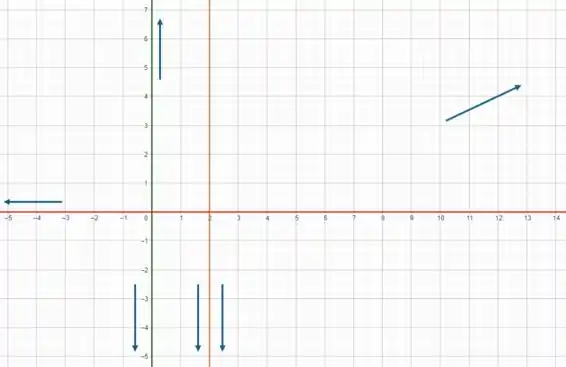
Com base nessas afirmações o gráfico de terá a seguinte característica.
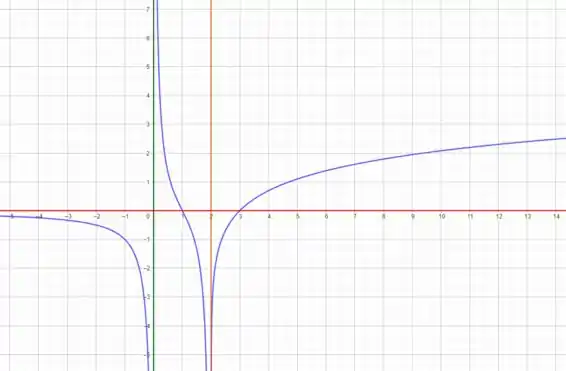
E aí! o que achou? Responde Aí! 😇
Resposta
