Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 72
69-73. A noção de assíntota pode ser estendida para incluir curvas não necessariamente retas. Especificamente, dizemos que as curvas e são assintóticas quando se:
E assintóticas quando se:
Nesses exercícios, determine uma função mais simples, tal que seja assintótica a quando ou . Use um recurso gráfico para gerar os gráficos de e de e identifique todas as assíntotas verticiais.
72.
Passo 1
Então pessoal, a princípio não se trata de uma questão tão simples de se interpretar, precisamos de bastante cuidado para não seguirmos caminhos errados aqui, ok? O que a questão quer é que encontremos uma função que seja assintótica quando ou quando . Como vamos descobrir essa função? Então, a saída mais tranquila é realizando a divisão de polinômios e em seguida caracterizando uma parte do resultado como a . Ficou complicado? Prometo que vai facilitar, se liga:
Dividindo os polinômios, teremos que:
Sendo assim, como deve ser assintótica, vamos chamar:
Até aqui tudo bem? Show de bola, bora continuar!
Passo 2
Utilizando o limite que o enunciado nos indica, teremos:
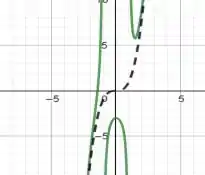
Sendo assim, podemos concluir que é assintótica para . Ademais, há duas assíntotas verticais no gráfico da função, que são em . Plotando isso, teremos:
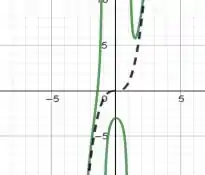
No qual a função em verde é e a função pontilhada é .
Resposta
Assíntotas Verticais:
