Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 7
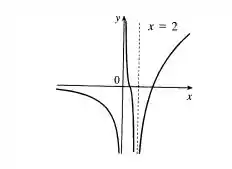
Esboce o gráfico de um exemplo de uma função que satisfaça todas as condições dadas
Passo 1
Bom galera, para resolver esse exercício, iremos elaborar um gráfico que satisfaça todas as condições apresentadas.
Passo 2
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de .
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de pela direita.
Passo 3
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de .
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de pela direita.
Para que satisfaça a condição
O nosso gráfico deverá ter no eixo o valor de conforme se aproxima de pela esquerda.
Resposta
