Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 13
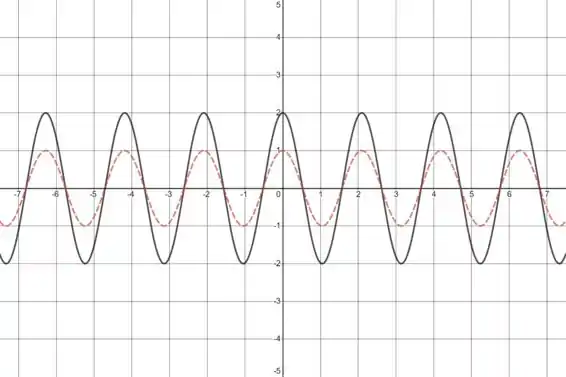
Faça o gráfico da função a mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.
Passo 1
Olá, meu querido estudante. Vamos dar início a mais uma resolução aqui.
A gente precisa criar um gráfico para a função:
A partir de um gráfico de outra função, e com os nossos conhecimentos de como constantes afetam o comportamento do gráfico de uma função.
Vamos utilizar como base o gráfico da função :
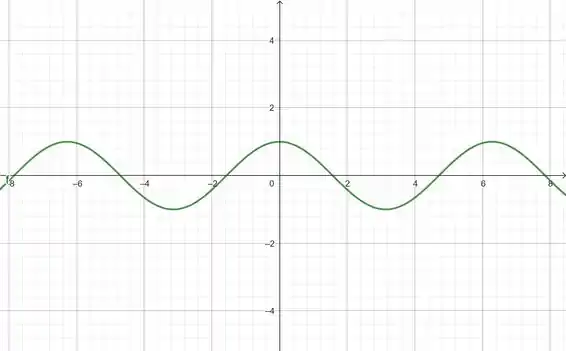
A partir dela que iremos encontrar o gráfico que queremos com as propriedades, certas.
Nesta seção 1.3, aprendemos que quando temos uma função do tipo devemos “alargar” a função na vertical, e quando temos o tipo devemos “encolher” a função na horizontal, isto é, deixar as oscilações mais estreitas.
Passo 2
O gráfico de é obtido pela contração horizontal do gráfico de por um fator de .
Portanto, se contraímos horizontalmente o gráfico de por um fator de , obteremos o gráfico de .
No gráfico abaixo:
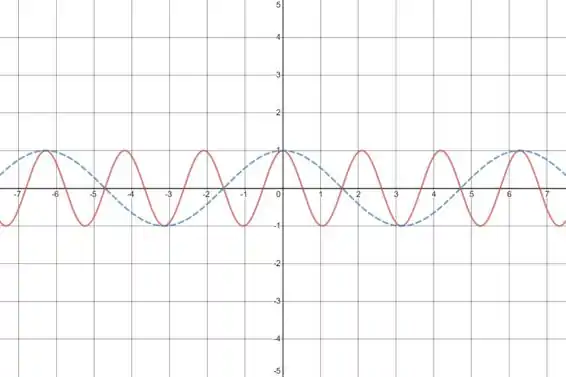
A curva tracejada azul representa .
A curva sólida vermelha representa .
O gráfico de é obtido esticando verticalmente o gráfico de por um fator de .
Portanto, se esticarmos verticalmente o gráfico de por um fator de , obteremos o gráfico de .
No gráfico abaixo:
A curva tracejada vermelha representa .
A curva sólida preta representa .
Resposta
