Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 29
Esboce o gráfico de uma função que satisfaça todas as condições dadas.
, para .
para . , .
para ou .
para , ,
Passo 1
Oieee, bom diaaa!
Vamos construir uma função que satisfaça todas as condições dadas:
(a derivada é zero em indicando um ponto crítico).
para a função é decrescente antes de
para (a função é crescente depois de
e (os pontos de inflexão estão em
para ou (a função é côncava para baixo fora do intervalo
para (a função é côncava para cima no intervalo
e (a função se aproxima de 3 quando tende ao infinito ou ao menos infinito).
Uma possível forma de que atenda a esses requisitos pode ser:
onde é uma função que ajuda a garantir os comportamentos desejados das derivadas primeiras e segundas.
Passo 2
Para simplificar, podemos optar por uma função polinomial ajustada com os comportamentos desejados em torno de pontos críticos e inflexão.
Podemos usar a função sigmoidal básica ajustada com uma correção polinomial:
onde é um polinômio que impõe as condições desejadas:
Para um ajuste preciso, podemos considerar:
Passo 3
Vamos verificar se esta função atende aos requisitos.
A função principal
possui limites assintóticos de 3 para
O termo polinomial:
Garante a formação dos pontos de inflexão e a mudança de concavidade desejada.
Vamos esboçar o gráfico da função
1. A função será decrescente para e crescente para
2. A função terá concavidade para cima entre e e concavidade para baixo fora desse intervalo.
3. Os pontos de inflexão estarão em
4. O valor da função se aproximará de 3 à medida que
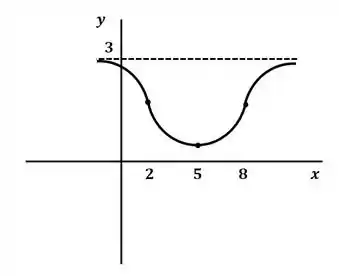
A função esboçada satisfaz todas as condições dadas:
- Crescente e decrescente conforme necessário.
- Pontos de inflexão em
- Limites assintóticos apropriados.
Resposta
Vide a explicação.