Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 49

Seja:

f ( x ) = 2 x 3 + x 2 - 15 x + 7 2 x - 1 3 x 2 + x - 1

Faça o gráfico de y = f ( x ) e econtre as equações de todas as assíntotas, horizontais e verticais. Explique por que não há assíntotas em x = 1 2 , mesmo que o denominador de f tenha um zero nesse ponto.

Passo 1

O gráfico pode ser dado por:

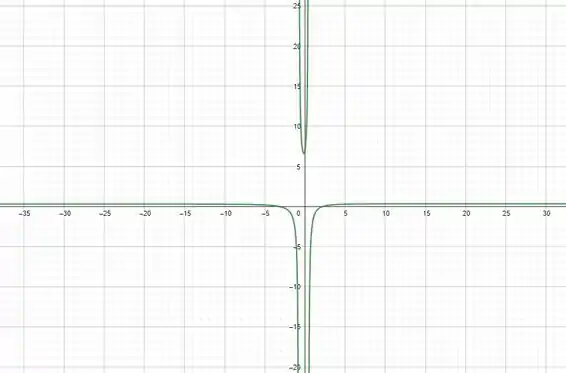
Passo 2

Vamos começar o exercício simplificando a função:

f ( x ) = 2 x 3 + x 2 - 15 x + 7 2 x - 1 3 x 2 + x - 1

Podemos reescrever:

2 x 3 + x 2 - 15 x + 7 = 2 x - 1 x 2 + x - 7

Substituindo na equação:

f ( x ) = 2 x - 1 x 2 + x - 7 2 x - 1 3 x 2 + x - 1

Cortando termos, temos:

f ( x ) = x 2 + x - 7 3 x 2 + x - 1

Agora, podemos calcular as assíntotas:

Passo 3

As assíntotas verticais podem ser calculadas nas indeterminações, ou seja, no ponto onde a função não existe. Isso acontece quando zeramos o denominador. Então, onde :

3 x 2 + x - 1 = 0

x = - b ± b 2 - 4 a c 2 a = - 1 ±   13 6

Ou seja, as assíntotas verticais são :

x = - 1 ±   13 6

Passo 4

No caso de x = 1 2 é uma raíz, e não é considerada uma assíntota.

Nesse caso, calcularemos o limite da função quando x = 1 2 :

lim x → 1 / 2 ⁡ 2 x 3 + x 2 - 15 x + 7 2 x - 1 3 x 2 + x - 1

Usando a função fatorada:

l i m x → 1 2 x 2 + x - 7 3 x 2 + x - 1 = 1 2 2 + 1 2 - 7 3 1 2 2 + 1 2 - 1 = 1 4 + 1 2 - 7 3 4 + 1 2 - 1 = - 25

O limite existe, se o limite fosse infinito, aí teria uma assíntota, nesse caso não há.

Resposta

Assintotas :

x = - 1 ±   13 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr
Faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos, de f ; os pontos de inflexão do gráfico de f ; os intervalos nos quais f é crescente aqueles onde f
Fazer um esboço do gráfico de f , determinando:. Os extremos relativos de f ;. Os pontos de inflexão do gráfico de f ;. Os intervalos onde f é crescente e aqueles nos quais f é decrescente;. Onde o gr
Verifique se as três condições da hipótese do teorema de Rolle estão satisfeitas pela função dada no intervalo indicado. Então, ache um valor adequado de c que satisfaça a conclusão do teorema de Roll
Faça um esboço do gráfico da função f dada, determinando primeiro o seguinte: os extremos relativos, de f ; os pontos de inflexão do gráfico de f ; os intervalos nos quais f é crescente aqueles onde f