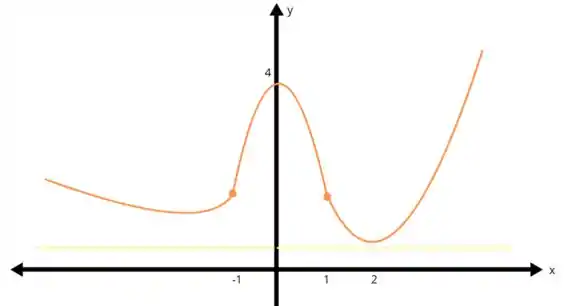
Suponha que é uma função contínua onde para qualquer valor de , , se ou , se , , se ou , se .
a) é possível que tenha um máximo absoluto? Em caso afirmativo, esboce um possível gráfico de , se não, explique o porque.
b) é possível que tenha um mínimo absoluto? Se sim, esboce um possível gráfico de , se não, explique o porque.
c) Esboce um possível gráfico de que não tenha um mínimo absoluto.
Passo 1
Opa! Blz?
Aqui temos aqui uma questão digna de mestre dos magos! A questão nos dá uma função misteriosa com as seguintes condições:
é uma função contínua
para qualquer valor de
se ou
se
se ou
se
Em cima disso temos que responder três perguntas! Bora encarar esse desafio?!
Vamos entender o que cada linha quer nos dizer
- é uma função contínua: não tem saltos ou quebras, e pode ser desenhada sem levantar o lápis do papel.
- para qualquer valor de : isso quer dizer que para qualquer valor de, essa função sempre estará na parte de cima do gráfico, onde é positivo.
- : O ponto que a função corta o é ,
- se ou : A derivada de , é positiva quando está à esquerda de ou à direita de . Isso significa que a inclinação da curva é positiva nessas regiões.
- se : A derivada de é negativa entre e . Portanto, a inclinação da curva é negativa nesse intervalo.
- : A segunda derivada de é zero nos pontos e . Isso indica que esses pontos podem ser pontos de inflexão na curva (onde a concavidade da curva muda).
- se ou : A segunda derivada de é positiva quando está à esquerda de ou à direita de . Isso sugere que a curva está côncava para cima nessas regiões (sorriso).
- se : A segunda derivada de é negativa entre e . Portanto, a curva é côncava para baixo nesse intervalo (triste).
Ufaaaa!
Agora que já destrinchamos o exercício, vamos responder às perguntas!

Passo 2
Na letra (a) ele pergunta se pode ter um máximo absoluto? Se sim, precisaremos esboçar um possível gráfico de , se não, temos que justificar.
Voltando na linha 7, do nosso passo a passo por linhas, percebemos que após e a função tem a concavidade para baixo (como um sorriso), e não temos mais mudanças após isso, assim ela continua crescendo conforme e , ou seja temos que a função é côncava para cima no intervalo e .
Dessa forma, podemos imaginar o gráfico da função sempre crescendo conforme avançamos no eixo , sendo assim, a função não pode ter um máximo absoluto.
Passo 3
A letra (b) é igual a letra (a), mas agora falando sobre o mínimo!
Através da condição da linha 7 se ou temos que a função é côncava para cima no intervalo , sabemos também de pela linha 5 que se e de se ou (pela linha 4) que a função decresce no intervalo e depois volta a crescer no intervalo .
Com base nas informações do enunciado, podemos concluir que a função é contínua em todos os pontos e tem concavidade para cima nos intervalos e , e concavidade para baixo no intervalo . Além disso, o gráfico de não apresenta quebras ou saltos no ponto
Dessa forma, o ponto pode ser um mínimo absoluto. O seguinte gráfico ilustra essa situação:
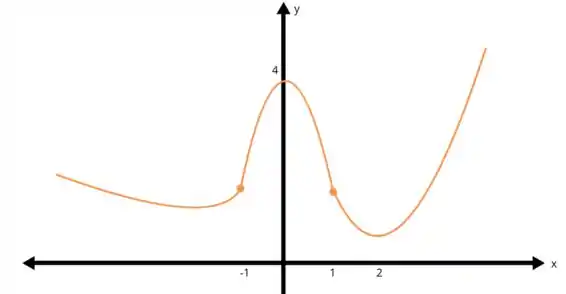
Passo 4
Agora vamos para a última etapa, a letra c). Temos que esboçar um possível gráfico de que não tenha um mínimo absoluto.
Para isso basta que modifiquemos o gráfico da letra b), deslocando a assíntota horizontal um pouco abaixo do ponto mínimo até então: . Podemos fazer com que o gráfico tenha uma assíntota em . Assim:
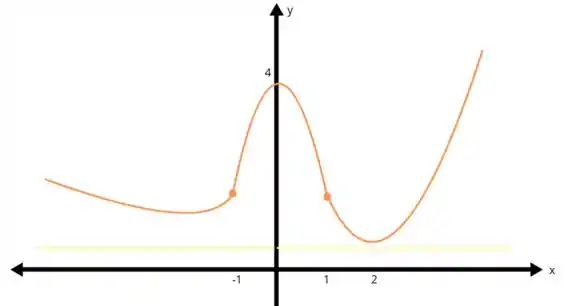
Prontinhooo!
Resposta
a) O gráfico da função é sempre crescente, sendo assim, a função não pode ter um máximo absoluto.
b)
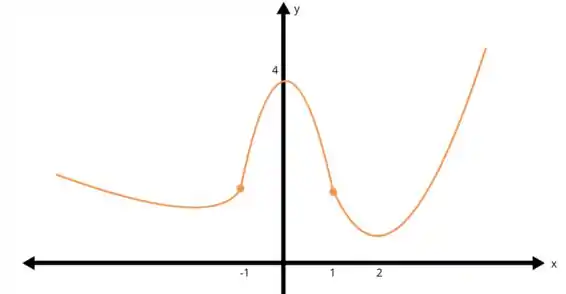
c)