Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 26
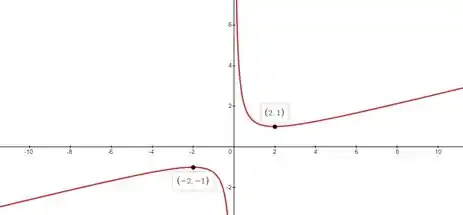
Esboce o gráfico de uma função que satisfaça a todas as condições dadas.
Assíntota vertical , se , se , se e se .
Passo 1
Eaeee, belezinha?? Bom... a questão quer que esbocemos o gráfico de uma função que satisfaça as seguintes condições:
- Assíntota vertical ;
- se ;
- se ;
- se ;
- se .
Eita... muita coisa né?
Mas calma... Como ele pediu pra gente mostrar apenas um gráfico e não a expressão da função, as coisas ficam um pouco mais fácil.
Mas basicamente a gente precisa saber do seguinte:
- Uma assíntota é uma linha ou curva que uma função se aproxima à medida que a variável independente se afasta para infinito ou para um ponto específico;
- A derivada primeira nos mostra o crescimento ou o decrescimento da função;
- A derivada segunda nos mostra a concavidade da curva.
Agora vamos aplicar!! 😉
Passo 2
Pra começar, vamos colocar uma assíntota em . Assim, a curva se aproxima do eixo mas nunca toca.
Para a primeira derivada temos o seguinte:
se
Então, será crescente para .
se
Assim, será decrescente para .
Passo 3
Para a segunda derivada:
se
Logo, nossa curva tem concavidade para baixo quando .
se
Portanto, nossa curva tem concavidade para cima quando .
Passo 4
Pra finalizar, basta esboçarmos um gráfico:
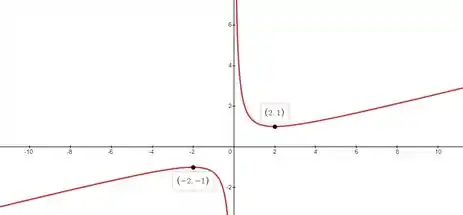
Entendeu direitinho?? Responde aee 😉
Resposta
