Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 65
Mostre que, de todos os triângulos isósceles com um dado perímetro, aquele que tem a maior área é o equilátero.
Passo 1
Nessa questão, queremos provar que entre todos os triângulos isósceles com determinado perímetro, o que possui maior área vai ser o equilátero.
Um triângulo isósceles é aquele que possui pelo menos dois lados iguais.
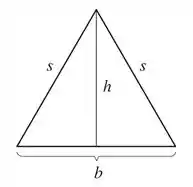
A área desse triângulo é dada por:
Usando Pitágoras, podemos escrever em funç��o de um dos lados.
Assim teremos a área em função de duas variáveis que são os lados do triângulo.
Para isso, precisamos encontrar uma função a qual queremos maximizar. Para encontrar o máximo dessa função, basta derivarmos e igualarmos a zero.
E como aqui nós só trabalhamos com uma única variável, caso tenhamos mais de uma variável (nesse caso, temos dois números que queremos encontrar) vamos usar uma equação de restrição para ter uma única variável.
Passo 2
Podemos esboçar o seguinte desenho:
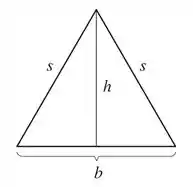
Nosso objetivo é achar a área máxima do triângulo isósceles com um dado perímetro e mostrar que ele é o equilátero, então primeiro, a fórmula da área:
Isolando uma das variáveis para substituir em (aqui eu estou usando Pitágoras, com um triângulo retângulo formado com , e , sendo a hipotenusa.
Substituindo:
Ainda temos dependendo de mais de uma variável, então vamos usar a informação do perímetro dada no enunciado para isolar uma delas:
Substituindo:
Agora nossa função depende apenas de . é uma constante.
Passo 3
Maximizando , para derivar eu estou usando a regra do produto.
Substituindo no perímetro:
Portanto, temos que:
Isso prova que todos os lados desse suposto triângulo são iguais, então ele é o triângulo equilátero.
Resposta
Desenvolvimento nos passos.