Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 24
Use o roteiro dessa seção para esboçar a curva:
Passo 1
Falai galerinha, tudo certo:
Como diria a Viúva Negra, “Ainda somos amigos, certo?”
Boraaa fazer essa comigo
A questão pede para esboçar a curva da função
Isso envolve entender a forma da curva, identificar pontos chave, e plotar o gráfico.
Para esboçar a curva de uma função, geralmente seguimos estes passos:
Identificar o domínio da função: Determinar para quais valores de a função é definida.
Calcular pontos chave: Como interceptos com os eixos
Determinar o comportamento assintótico: Verificar o comportamento da função quando tende a
Derivar a função: Encontrar a derivada para determinar os pontos críticos e a concavidade da curva.
Plotar o gráfico: Usar as informações obtidas para desenhar a curva.
Passo 2
Domínio da Função:
Para
Ser definida, o argumento da raiz quadrada deve ser maior ou igual a zero:
Interceptos:
- Intercepto com o eixo
- Interceptos com o eixo
Derivada da Função:
Para encontrar pontos críticos e determinar a concavidade:
Comportamento Assintótico:
Analisar o comportamento da função quando tende a
Passo 3
Domínio:
A solução é
Interceptos:
Para
Para
Elevando ao quadrado ambos os lados:
Derivada:
Usando a regra da cadeia e a regra do quociente:
Passo 4
Vamos encontrar os pontos críticos resolvendo
Elevando ao quadrado ambos os lados:
Isso mostra que não há pontos críticos distintos dos já conhecidos.
Passo 5
O gráfico da função
Foi plotado e apresenta as seguintes características:
-*Domínio: A função está definida para
Esses intervalos foram considerados ao plotar o gráfico.
- Interceptos: A função intercepta o eixo no ponto
- Comportamento: Para , a curva começa alta e desce suavemente conforme
se aproxima de -1.
Para a curva começa no ponto e sobe conforme aumenta.
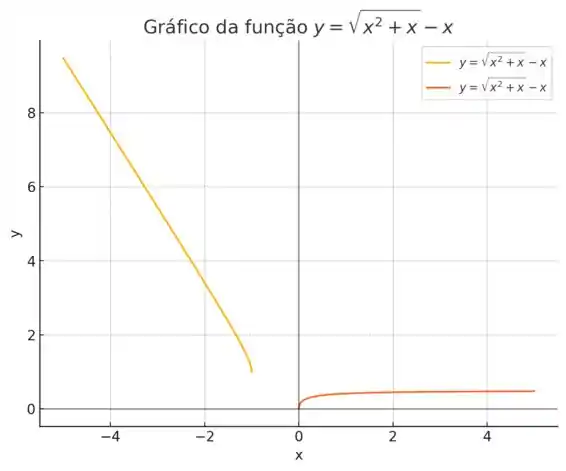
- No intervalo a função apresenta valores positivos que diminuem em magnitude à medida que se aproxima de
- No intervalo a função começa do zero e aumenta conforme cresce.
- A função não é definida no intervalo devido ao domínio
O gráfico oferece uma visualização clara do comportamento da função nos intervalos definidos.
“Nós somos Groot”
Resposta
Vide o passo a passo.