Esboce o gráfico de uma função que seja contínua em e tenha as propriedades dadas:
Máximo absoluto em , mínimo absoluto em , máximo local em e mínimo local em e .
Passo 1
Devemos esboçar o gráfico de uma contínua (sem buracos ou saltos) no intervalo e os máximo e mínimo globais sejam, respectivamente, e e, além disso, tenha dois extremos locais: um mínimo em e um máximo em . Como devemos ter um mínimo local em também, o mínimo absoluto deve ser local também.
Passo 2
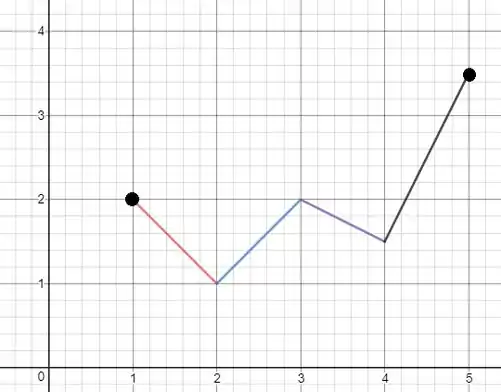
Um gráfico que satisfaz todas as propriedades é:
Resposta
Esboço de gráfico.