Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.1 - Ex. 10
Esboce o gráfico de uma função que seja contínua em e tenha as propriedades dadas:
não tem máximos e mínimos locais, mas e são números críticos.
Passo 1
Eaeee, belezinha?? Bom...Precisamos esboçar o gráfico de uma função contínua no intervalo e que não tenha extremos locais.
Assim, devemos esboçar o gráfico de uma função crescente ou decrescente.
Todavia, e devem ser pontos críticos, porém eles não podem ser extremos locais!!!
Uma forma de um ponto crítico não ser extremo local é se ele for um ponto de inflexão: um ponto onde a derivada se anula e a segunda derivada também se anula.
Passo 2
Desenhamos um gráfico que satisfaz as propriedades dadas com dois pontos de inflexão:
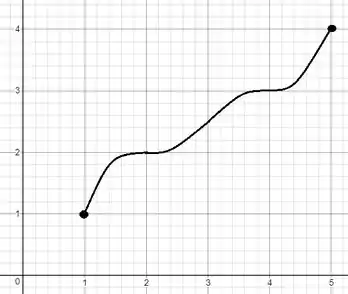
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x + 1 x 2 + 2 x + 2
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x x 2 + 1
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = cos - 1 ( x ² ) ²
Determine os pontos críticos,extremidades de domínio e valores extremos (absolutos e locais) da função: y = x 2 3 ( x + 2 )
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = e x + e - x