Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 16
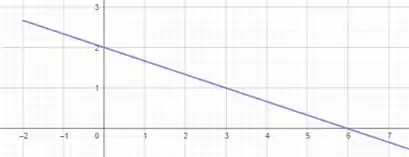
Esboce o gráfico de à mão e use seu esboço para encontrar os valores máximos e mínimos locais e absolutos de . (Use os gráficos e as transformações das Seções 1.2 e 1.3.)
Passo 1
Eaee, belezinha?? Seguinte... O problema nos dá a seguinte função:
Temos que esboçar essa curva e depois devemos usá-lo para acharmos os valores de máximos e mínimos locais e absolutos.
Para isso, temos que utilizar os gráficos e as transformações das Seções 1.2 e 1.3.
Bora lá?! 😉
Passo 2
Veja que trata-se de uma reta.
Assim, podemos sair da função:
E fazer:
Segundo as transformações vista no capítulo 1.3 do livro, nesse caso comprimimos o gráfico horizontalmente por um fator de , nesse caso .
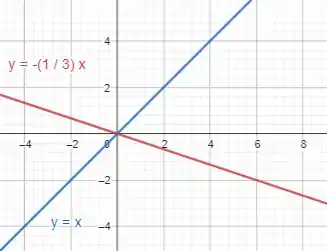
Passo 3
Agora temos a transformação:
Nesse caso deslocamos o gráfico pra cima em unidades:
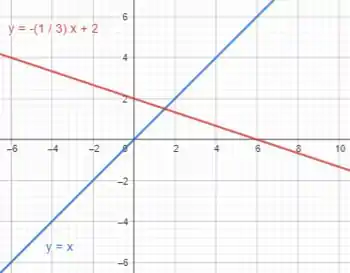
Assim, temos o gráfico (aplicando a condição ):
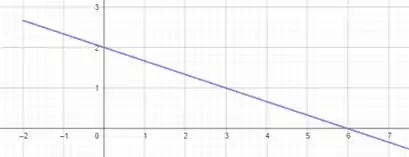
Passo 4
Vemos que o ponto máximo então é e não temos pontos mínimos, pois a função só está limitada superiormente, com a condição de que .
Sendo assim:
Ponto máximo local: não tem.
Ponto máximo absoluto:
Ponto mínimo local: não tem
Ponto mínimo absoluto: não tem.
Resposta
Apenas ponto máximo absoluto:
