Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 59
(a) Use um gráfico de para estimar os valores máximo e mínimo. Então, encontre os valores exatos.
(b) Estime o valor de em que cresce mais rapidamente. Então, encontre o valor exato.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente usar o gráfico da função para estimar os valores de máximo e mínimo locais e estimar também o valor de em que a função cresce mais rapidamente. Em seguida, nós vamos encontrar um valor exato para essas estimativas.
Beleza, então vamos precisar do gráfico de :
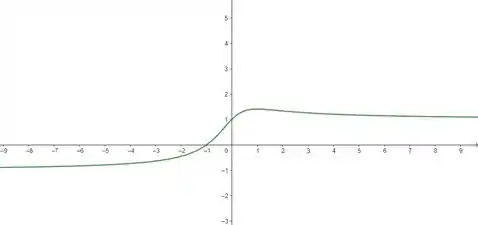
Com ele, nós vamos verificar se existem “picos” ou “vales”, que representariam pontos de máximo e mínimo da função. Então, nós vamos calcular o valor exato dessa estimativa usando a derivada da função em seus pontos críticos ().
Além disso, nós vamos verificar em que intervalo essa função tá crescendo mais rápido. Isso significa que vamos verificar o máximo valor da derivada, que é a máxima taxa de variação desse crescimento. Nós fazemos isso calculando a segunda derivada da função e igualando o resultado a zero ().
Vamos lá!
Passo 2
Olhando lá no nosso gráfico do passo , a gente percebe que em temos um ponto de máximo local:
Mas a gente percebe também que não existem pontos de mínimo na curva dessa função. Então, vamos verificar se isso é verdade, calculando os pontos críticos da função.
Derivando , usando a regra do quociente, temos:
Igualando esse resultado a zero, para encontrar os pontos críticos:
E como o denominador não pode ser zero, temos apenas:
Isolando :
Portanto, é o único ponto crítico da função. Substituindo ele em , temos:
E a raiz de dois é aproximadamente igual a , portanto, nossa estimativa estava correta.
Passo 3
Beleza, agora olhando novamente para o gráfico, percebemos que ele cresce mais rapidamente mais ou menos entre e . Para encontrar o valor exato, nós precisamos encontrar o valor máximo de . Fazemos isso, encontrando os valores críticos de . Ou seja, vamos derivar a função novamente e igualar esse resultado a zero.
Derivando , usando a regra do quociente, temos:
Igualando esse resultado a zero:
Como o denominador não zera, temos:
Encontrando as raízes dessa equação do segundo grau, vamos obter:
Onde corresponde ao mínimo valor de . E o máximo valor de vai ocorrer em , que é bem próximo do valor que estimamos no gráfico.
Valeu, galera! Até a próxima! 😉