Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 21
Esboce o gráfico possível de uma função com as propriedades especificadas. (São possíveis muitas soluções diferentes)
21.i) o domínio de é [-1, 1]
ii)
iii)
Passo 1
Aqui, podemos imaginar várias possibilidades de funções, as quais quisermos, pra esboçar, dentro das propriedades especificadas. Assim, as possibilidades mais fáceis vão ser a nossa prioridade pra resposta.
Passo 2
i)Aqui, vale absolutamente qualquer função, contínua, dentro do intervalo estabelecido. Como resposta possível, pegamos esse intervalo da função :
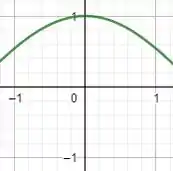
Passo 3
ii)Aqui, uma possibilidade muito simples é a função :
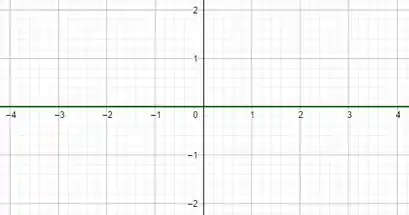
Passo 4
iii)Aqui, igualmente simples, podemos usar a função .
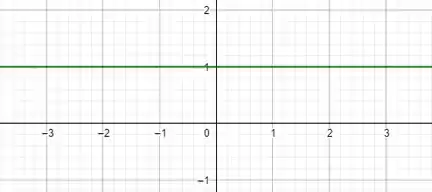
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
É dado lim x → a f x = L . Determine um número δ para o ε dado tal que f x - L ε sempre que 0x - aδ . Dar exemplos de dois outros números positivos para δ , que também satisfazem a implicação dada.
Para a função cujo gráfico está na figura abaixo, encontre lim x → 0 - G ( x ) (b) lim x → 0 + G ( x ) (c) lim x → 0 G ( x ) (d) G ( 0 )
Para a função cujo gráfico está na figura abaixo, encontre(a) lim x → 2 - f ( x ) (b) lim x → 2 + f ( x ) (c) lim x → 2 f ( x ) (d) f ( 2 )
Para a função cujo gráfico está na figura abaixo, encontre(a) lim x → 0 - G ( x ) (b) lim x → 0 + G ( x ) (c) lim x → 0 G ( x ) (d) G ( 0 )
Para a função cujo gráfico está na figura abaixo, encontre lim x → 0 - g ( x ) (b) lim x → 0 + g ( x ) (c) lim x → 0 g ( x ) (d) g ( 0 )