Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.1 - Ex. 26
Esboce o gráfico possível de uma função com as propriedades especificadas. (São possíveis muitas soluções diferentes)
26.i)
ii) e
iii) e
Passo 1
Aqui, podemos imaginar várias possibilidades de funções, as quais quisermos, pra esboçar, dentro das propriedades especificadas. Assim, as possibilidades mais fáceis vão ser a nossa prioridade pra resposta.
Passo 2
i)Um bom exemplo de função é a função módulo, mas um pouco modificada: a função , que vai fazer valer o pedido do enunciado:
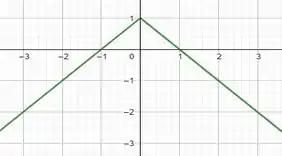
Passo 3
ii)Pra esse caso, as coisas já complicam um pouco, e se você tem um bom domínio de pré-cálculo e de funções, talvez fique um pouco mais tranquilo. Uma função que pode servir pra gente é a . Tem o seguinte gráfico:
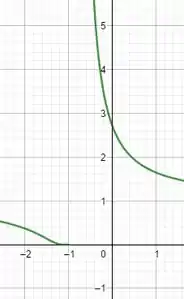
Passo 4
iii)Aqui, o mesmo que logo acima: fica mais complicado, mas tendo conhecimento de manipular funções, adicionando ou subtraindo algumas unidades da variável ou da lei da função como um todo, dá pra chegar a um resultado.
Pro caso, temos a função :
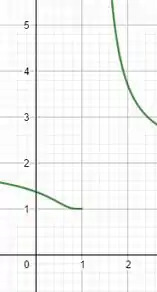
Resposta
Ei, a resposta está no passo a passo :)