Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.2 - Ex. 49
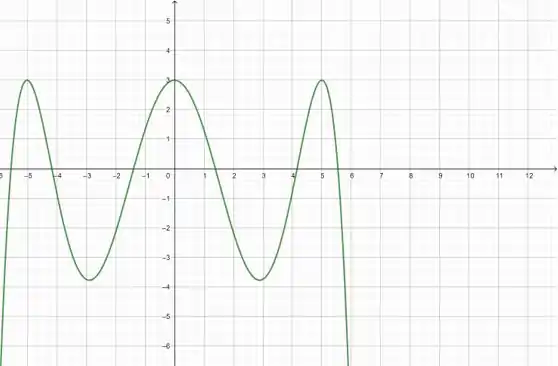
Esboce o gráfico de , para as funções abaixo:
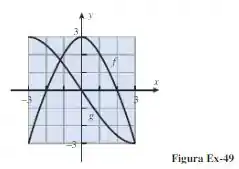
Passo 1
Para fazer uma gráfico de precisamos saber que funções são essas, certo? Para, depois, achar a composição delas.
Para achar que funções são essas, vamos ter que ver com que estilo de função elas se parecem a partir do gráfico que foi dado:
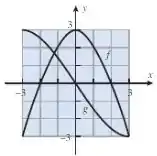
Vamos tentar achar a equação de primeiro. Olhando para o gráfico de , vemos que ela se parece muito com uma parábola, pois tem apenas uma curva bem definida ali, um ponto que poderia ser o vértice e outros dois e que seriam as raízes. Sendo assim, ela vai ter essa cara:
Que é a cara clássica de uma parábola, ok? Vamos pegar esses 3 pontos citados anteriormente, jogar tudo nessa equação para e achar os valores de , e , show? Vamos lá!
Primeiro, substituindo o ponto de :
Daqui, tiramos que:
Substituindo :
Substituindo :
Substituindo nas duas, temos o seguinte sistema para resolver:
Somando as duas equações:
Substituindo na primeira equação:
Isolando :
Com isso:
Vamos plotar esse gráfico para ver se bate com o da imagem:
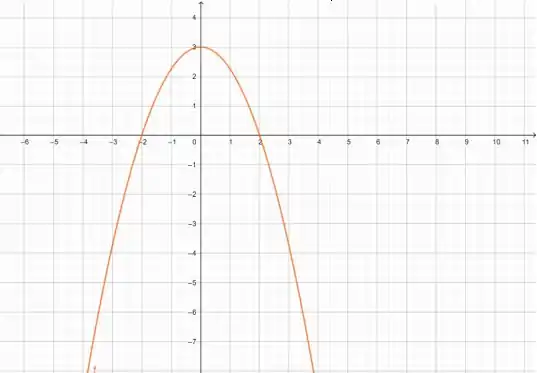
Deu certinho!
Passo 2
Agora, vamos tentar achar :
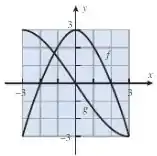
Olhando, de novo, para a imagem, vemos que tem um comportamento diferente do de . Ela tem duas concavidades ali, uma com o vértice em e outra em . Cara, quando temos algo desse tipo, podemos pensar em uma função com um grau a mais que a parábola, ou seja, uma função do terceiro grau:
Onde temos uma raiz em e um ponto :
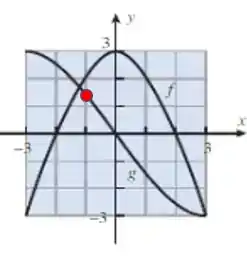
Beleza, vamos trabalhar em cima dos 4 pontos que vimos.
Substituindo :
Daqui, tiramos que:
Substituindo :
Arrumando e substituindo :
Substituindo
Arrumando e substituindo :
Então, temos 2 equações:
Se a gente soma as duas equações:
Vamos substituir esse valor nas outras equações:
Temos um problema, se somarmos essas equações, chegamos a:
Calma, temos mais um ponto! Substituindo :
Arrumando e substituindo os valores que temos:
Juntando à outra equação:
Vamos multiplicar a primeira por 3:
Somando as duas:
Simplificando por 1,5:
Substituindo o valor na primeira equação:
Fazendo o mmc, que é 80:
Simplificando por 5:
Dessa forma:
Olha só as duas funções:
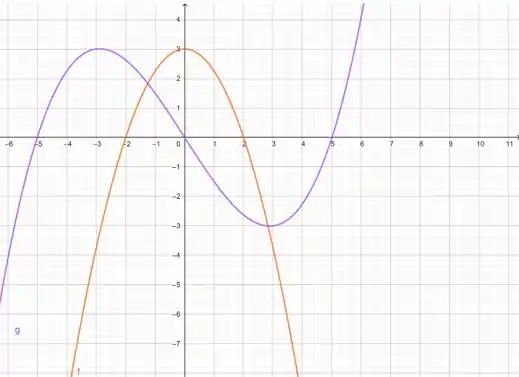
Pôoo, vai me dizer que não ficou igual à imagem do enunciado? Muito bom!
Passo 3
Agora, vamos fazer a composição , substituindo de por :
Então:
Olha, isso vai dar uma função do sexto grau... Relaxa que é completamente normal não saber esboçar essa curva, tá? Até porque é beeemmm difícil pedirem isso em algum lugar. A não ser que você já tenha visto alguma coisa de cálculo, como limite e derivada. Mas, até essa parte do livro, ninguém viu isso ainda. Então, vamos nos poupar de contas e usar um recurso gráfico, ok?
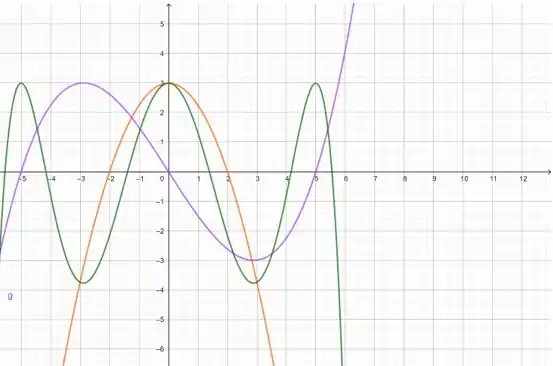
Olha essa composição em verde....... Falei que ficaria estranho kkk. Mas tudo bem, mas deixar só ela agora:
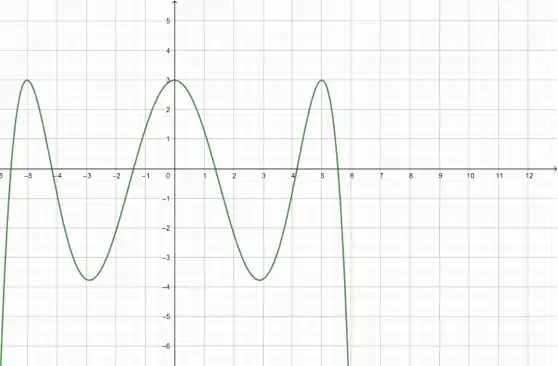
Prontinho! É isso.
Resposta
