Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.4 - Ex. 31
Faça o gráfico da função , , para . Como varia o gráfico com o crescimento de ?
Passo 1
A questão pede para plotarmos o gráfico da função , com , para diversos valores inteiros de indo de até .
A função é dada pela multiplicação de uma função exponencial negativa com uma função potência .
Dessa forma, ao mudarmos os valores de indo de até , estamos aumentando o grau da nossa função potência.
Passo 2
A seguir fazemos os plots de todas as funções.
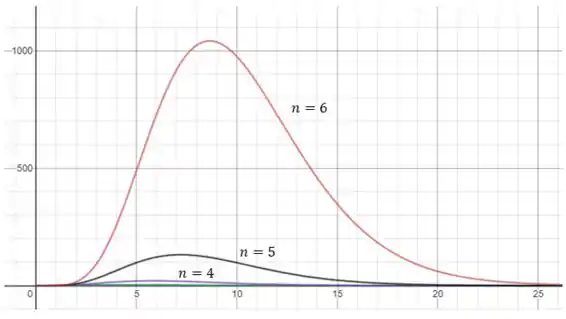
Repara que como algumas funções ficaram maiores que as outras, não conseguimos visualizar o que ocorre, dessa forma, vou dar um zoom para vermos as funções menores.
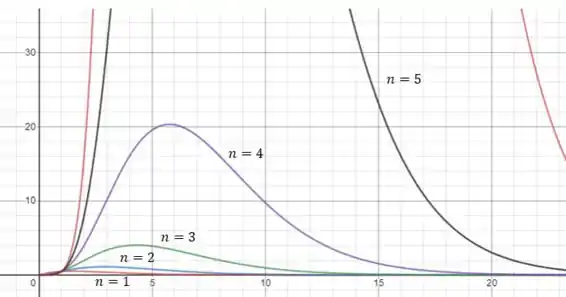
Conforme aumenta, o pico da curva aumenta. Além disso, o pico da curva ocorre para valores maiores de a medida que o aumenta.
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
Encontre todas as soluções da equação, com duas casas decimais de precisão. x 2 = s e nx
Os gráficos se interceptam na janela retangular dada? Se eles se interceptarem, quantos pontos de interesecção existem? y = 6 - 4 x - x 2 ,y = 3 x + 18 ; - 6 ,2p o r [ - 5 ,20 ]
Faça o gráfico da hipérbole y 2 - 9 x 2 = 1 por meio dos gráficos das funções que são os ramos superior e inferior da hipérbole.
O que acontece com o gráfico da equação y 2 = c x 3 + x 2 à medida que c varia?
Os gráficos se interceptam na janela retangular dada? Se eles se interceptarem, quantos pontos de interesecção existem? y = 3 x 2 - 6 x + 1 ,y = 0,23 x - 2,25 ; - 1 ,3p o r [ - 2,5 ,1,5 ]