Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 39
Encontre a altura e o raio de um cone circular reto com o menor volume que pode circunscrever uma esfera de raio .
Passo 1
Então pessoal, a fim de facilitar nossa visualização sobre o problema, temos a seguinte situação:
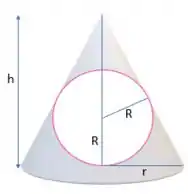
Vamos chamar a altura do cone de , o raio da esfera de e o raio do cone de , tudo jóia? Show! Como sabemos, o volume do cone é:
Se utilizarmos semelhança de triângulos, teremos o seguinte:
No qual essa raíz do denominador aparece por conta do teorema de Pitágoras. Se isolarmos , teremos:
Substituindo na expressão de :
Agora deixamos a expressão de em função apenas de e não mais em função de e !
Passo 2
Como o enunciado fala de minimizar o volume, então temos que encontrar os pontos críticos da nossa função, ou seja:
Simplificando, teremos:
Igualando nossa derivada a zero:
As únicas formas disso dar zero são se:
Ou:
Como não pode ser zero, então temos que nosso resultado é !
Passo 3
Agora que encontramos , para descobrirmos é tranquilo, pois basta utilizarmos a expressão que encontramos no passo 1, se liga:
Para temos que será:
E está aí nossa resolução, pessoal! 😊