Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.4 - Ex. 38
Encontre as dimensões do triângulo isósceles de menor área que pode circunscrever um círculo de raio .
Passo 1
Então galera, a fim de facilitar a visualização do problema, vamos esboçar como seria essa coisa toda aí, se liga:
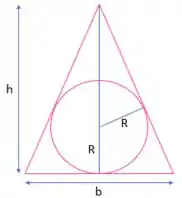
Então temos o seguinte: é a altura do triângulo, é o raio do círculo e é a base do triângulo. Para um triângulo qualquer, temos que a área é:
Além disso, por semelhança de triângulos conseguimos tirar o seguinte:
Vale ressaltar que essa raíz sai do teorema de Pitágoras, ok? Isolando na expressão que acabamos de criar, teremos:
Isolando na expressão de :
Show!
Passo 2
O enunciado quer um triângulo com dimensões mínimas, então temos que utilizar os conceitos de cálculo que aprendemos! Para encontrarmos mínimo a partir da expressão de que escrevemos, devemos derivar a função e igualar a zero, saca só:
Simplificando:
Igualando nosso resultado a zero:
Para isso dar zero existem duas possibilidades:
Ou:
Como não pode ser zero, o único resultado aceitável seria . Ok, encontramos uma das duas dimensões!
Passo 3
Agora que encontramos , devemos encontrar . De acordo com o que deduzimos no passo , temos:
Substituindo :
E estão aí as dimensões procuradas pelo enunciado, galera! 😉