Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.3 - Ex. 46
Esboce a região delimitada pela curva fornecida e calcule sua área:
, ,
Passo 1
Tudo bão?
Vamos para mais um exercício, agora temos uma região que segue as seguintes regras:
O problema nos deu a faca e queijo na mão, e você já vai entender como resolver.
Vamos lá!
Então desenhando todas as nossas restrições temos:
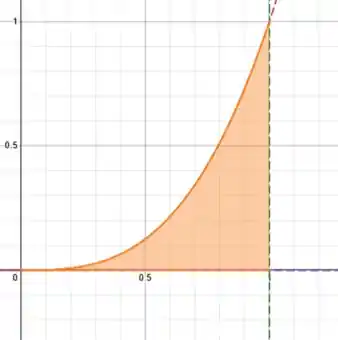
Então olhando da esquerda para direita, nossa área é limitada por e , como a integral é a área acima do , queremos então a área abaixo de , no trecho que até .
E olha só! Temos a definição de uma integral!
Agora sim, vamos calcular!
Passo 2
Como vimos no passo 1, a forma da nossa integral essa área é:
Passo 3
Beleza, agora vamos calcular o resultado da integral usando a regra geral:
Como temos uma potência:
Aplicando no nosso problema, temos:
Agora aplicando o Teorema Fundamental do Cálculo:
O Teorema Fundamental do Cálculo diz que se você tem uma função que não tem buracos e é suave (ou seja, contínua) entre dois pontos e , então a integral definida dessa função de até é o mesmo que a diferença entre as primitivas(integrais) nos limites de integração.
Aqui teremos e .
E essa é a área que estamos procurando!
