Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 7e
Em cada um dos itens a seguir, calcular a integral da função no intervalo dado e esboçar seu gráfico.
Passo 1
Vamos esboçar primeiro. O gráfico é esse:
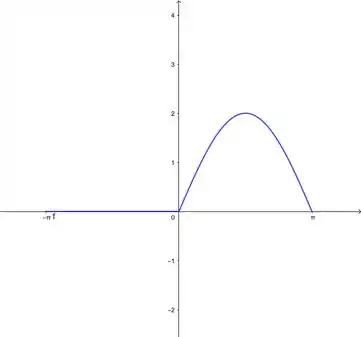
Passo 2
Vamos integrar a função agora. Vai ficar assim:
Nesse caso a gente vai ter que separar em uma parte positiva e outra negativa...
Prontinho! Essa é a integral😉
Resposta
Exercícios de Livros Relacionados
Use o Teorema de Pappus e o resultado do Exercício 39 para calcular o volume do sólido gerado quando a região limitada pelo eixo x e o semicírculo y = a 2 - x 2 gira em torno da (b) reta y=x-a
Use o Teorema de Pappus e o resultado do Exercício 39 para calcular o volume do sólido gerado quando a região limitada pelo eixo x e o semicírculo gira em torno da (a) reta y=-a
Como podemos reconhecer se um problema pode ser resolvido utilizando o Teorema de Pappus? Ou seja, quais são as “pistas” e as “incógnitas” que poderiam sugerir uma tal solução? Discuta dois ou três ex
Use o Teorema de Pappus e o fato de que a área de uma elipse com semieixos a e b é π a b para calcular o volume do toro elíptico gerado pela revolução da elipse x - k 2 a 2 + y 2 b 2 = 1 em torno do e
Use um CAS para encontrar a massa e o centro de gravidade da lâmina dada de densidade δ .A lâmina delimitada por y = e x , y = 0 , x = 0 e x = 1 ; δ = 1 e - 1 .