Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 6.1 - Ex. 6
Esboce a região delimitada pelas curvas dadas. Decida quando integrar com relação a ou a . Desenhe um retângulo aproximante e coloque sua altura e largura. Então calcule a área da região.
Passo 1
Fala aí! tudo certinho?
A questão pede para fazermos um desenho da região para, assim, decidir a melhor forma de fazer a integração para calcular a área.
Para calcular a area entre duas curvas, fazemos
O desenho da região é feito a seguir:
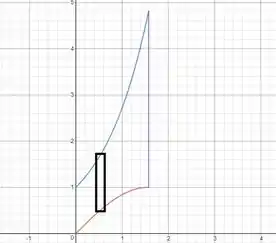
A largura do retângulo será (então a integral será feita em ) e sua altura será a diferença entre as funções, no caso .
Assim, a área da região será
Veja só!
Passo 2
Efetuando a integral:
Aplicando os limites de integração...
E aí! o que achou? Responde Aí!
Resposta
Exercícios de Livros Relacionados
Determine a área das regiões delimitadas pelas curvas e retas x = 2 y 2 ,x = 0,y = 3
Determine a área das regiões delimitadas pelas curvas e retas y = s e n x , y = x,0 ≤ x ≤ π 4
Determine a área da região” triangular” no primeiro quadrante , limitada à esquerda porx + y = 2 , à direita por = x 2 e acima por y = 2
Determine a área das regiões delimitadas pelas curvas e retas y = 2 s e n x , y = s e n ( 2 x ),0 ≤ x ≤ π
Determine a área das regiões delimitadas pelas curvas e retas x = 4 - y 2 ,x = 0